Rumusrumus.com kali ini akan membahas wacana kekerabatan matematika dan klarifikasi dari aneka macam macam kekerabatan matematika serta akan dibahas juga perbedaan antara kekerabatan dan fungsi matematika dan pola soal relasi.
Pengertian Relasi
Relasi yaitu korelasi antara anggota pada suatu himpunan dengan anggota himpunan yang lainya. Relasi dari himpunan A ke himpunan B ialah menghubungkan anggota-anggota himpunan A pada anggota-anggota himpunan B.
Cara Menyatakan Relasi
Relasi dua himpunan A dan himpunan B dapat dinyatakan dengan 3 cara yaitu :
- Diagram panah
- Diagram cartesius
- Himpunan pasangan berurutan.
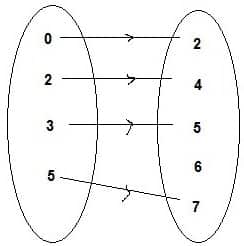
1. Diagram Panah
Anggota-anggota himpunan P ber kekerabatan dengan anggota himpunan Q dengan kekerabatan “menyukai”. Hal itu ditunjukkan dengan arah panah. Oleh alasannya yaitu itu, diagramnya disebut diagram panah.
Contoh :
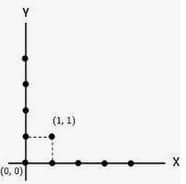
2. Diagram Cartesius
Diagram Cartesius merupakan diagram yang terdiri dari sumbu X dan sumbu Y. Pada diagram kartesius, anggota himpunan P terletak pada sumbu x, sedangkan anggota himpunan Q terletak pada sumbu y Relasi yang menghubungkan himpunan P dan Q ditunjukkan dengan noktah ataupun titik.
Contoh :
3. Himpunan Pasangan Berurutan
Sebuah kekerabatan yang menghubungkan himpunan yang satu dengan himpunan lainnya dapat disajikan pada bentuk himpunan pasangan berurutan. Cara penulisannya yaitu anggota himpunan P ditulis pertama, sedangkan anggota himpunan Q menjadi pasangannya.
Contoh :
{(Rani, basket)}, {(Rani, bulu tangkis)}, {(Dian, basket)}, {(Dian, atletik)}, {(Isnie, senam)}, {(Dila, basket)}, {(Dila, tenis meja)}
Sifat – Sifat Relasi
Sebuah kekerabatan A×A, yaitu kekerabatan dari himpunan A kepada A sendiri, memiliki sifat-sifat berikut:
- Refleksif
- Irefleksif
- Simetrik
- Anti-simetrik
- Transitif
Di sebut kekerabatan R dari A kepada A sebagai kekerabatan R dalam A.
Jenis-Jenis Relasi
- Relasi Simetrik
- Relasi anti Simetrik
- Relasi Transitif
- Relasi Refleksif
- Relasi Invers
1. Relasi Invers
Misalkan R yaitu kekerabatan dari himpunan A ke himpunan B. Invers dari R yang dinyatakan dengan kekerabatan dari B ke A yang mengandung semua pasangan terurut yang apabila dipertukarkan masih termasuk dalam R. Ditulis dalam notasi himpunan sebagai berikut ; R-1= {(b,a) : (a,b)R}
Contoh:
A = {1,2,3} B = {x,y}
R = {(1,x), (1,y), (3,x)} kekerabatan dari A ke B
R-1= {(x,1), (y,1), (x,3)} kekerabatan invers dari B ke A
2. Relasi Simetrik
Misalkan R = (A, B, P(x,y)) suatu relasi. R disebut kekerabatan simetrik, kalau tiap (a,b)R berlaku (b,a)R. Dengan istilah lain, R disebut juga kekerabatan simetrik kalau a R b berakibat b R a.
Contoh Relasi Simetrik :
perhatikan satu per satu. Setiap kali kau menemukan pasangan, contohnya (a, b), maka cari apakah (b, a) juga ada. Kalau ternyata tidak ada, niscaya kekerabatan itu tidak simetrik.
3. Relasi Refleksif
Misalkan R = (A, A, P(x,y)) suatu relasi. R disebut kekerabatan refleksif, kalau setiap A berlaku (a,a)R. Dengan kata lain, R disebut kekerabatan refleksif kalau tiap-tiap anggota pada A berelasi dengan dirinya sendiri
Contoh :
Relasi Refleksif Diketahui A = {1, 2, 3, 4} dan R = {(1,1), (2,3), (3,3), (4,2), (4,4)} Apakah R kekerabatan refleksif ? R bukan kekerabatan refleksif, karna (2,2) tidak termasuk dalam R. Jika (2,2) termasuk dalam R, yaitu R1= {(1,1), (2,2), (2,3), (3,3), (4,2), (4,4)} maka R1 merupakan kekerabatan refleksif.
4. Relasi anti Simetrik
Suatu kekerabatan R dapat disebut kekerabatan anti simetrik andai (a,b)R dan (b,a)R maka a=b. Dengan kata lain Jika a, b A, a≠b, maka (a,b)R atau (b,a)R, tetapi tidak kedua-duanya.
Contoh :
Misalkan R suatu kekerabatan pada himpunan bilangan orisinil yang didefinisikan “y habis dibagi oleh x”, maka R merupakan kekerabatan anti simetrik alasannya yaitu kalau b habis dibagi a dan a habis dibagi b, maka a = b.
Misalkan A = {1, 2, 3} dan R1= {(1,1), (2,1), (2,2), (2,3), (3,2)}, maka R1bukan kekerabatan anti simetrik, alasannya yaitu (2,3)R1dan (3,2)R1.
5. Relasi Transitif
Misalkan R kekerabatan dalam himpunan A. R disebut kekerabatan transitif kalau berlaku ; (a,b)R dan (b,c)R maka (a,c)R. Dengan kata lain andai a berelasi dengan b dan b berelasi dengan c, maka a berelasi dengan c.
Contoh :
Misalkan A = {a, b, c} dan R = {(a,b), (a,c), (b,a), (c,b)}, maka R bukan kekerabatan transitif, alasannya yaitu (b,a)R dan (a,c)R tetapi (b,c)R. dilengkapi biar R menjadi kekerabatan transitif R = {(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)}
Perbedaan Relasi da Fungsi
Secara sederhana, kekerabatan dapat diartikan sebagai hubungan. Hubungan yang dimaksud di sini yaitu korelasi antara kawasan asal (domain) dan kawasan mitra (kodomain).. Sedangkan fungsi yaitu kekerabatan yang memasangkan tiap anggota himpunan kawasan asal sempurna satu ke himpunan kawasan kawannya.
Perbedaan antara kekerabatan dan fungsi ada pada cara memasangkan anggota himpunan ke kawasan asalnya.
Pada relasi, tidak ada hukum yang khusus untuk memasangkan setiap anggota himpunan kawasan asal ke kawasan kawan. Aturan hanya terikat atas pernyataan kekerabatan itu sendiri. Setiap anggota himpunan kawasan asal boleh memiliki pasangan lebih dari satu atau boleh juga tidak memiliki pasangan.
Sedangkan pada fungsi, tiap-tiap anggota himpunan kawasan asal dipasangkan dengan hukum khusus. Aturan itu mengharuskan setiap anggota himpunan kawasan asal memiliki pasangan dan hanya sempurna satu dipasangkan dengan kawasan kawannya.
Kesimpulannya, setiap kekerabatan belum tentu fungsi, namun setiap fungsi niscaya merupakan relasi
Contoh Soal Relasi Matematika
Contoh Soal 1
Himpunan P = {2, 3, 4, 6} dan Q = {1,2,3,4,6,8} dan “faktor dari” merupakan kekerabatan yang menghubungkan antara himpunan P ke himpunan Q . Buatlah kekerabatan ke bentuk himpunan pasangan berurutan.
Jawab :
{(2,2)}, {(2,4)}, {(2,6)}, {(2,8)}, {(3,3)}, {(3,6)}, {(4,4)}, {(4,8)}, {(6,6)}
Contoh Soal 2
jika siska menyukai sepakbola, liya menyukai voli dan basket dan berli menyukai basket dan sepakbola. buatlah kekerabatan himpunan pasangan berurutan .
penyelesaian :
{(Siska,sepakbola)}, {(liya,voli)}, {(liya,basket)}, {(berli,basket)}, {(berli,sepakbola)}
Contoh Soal 3
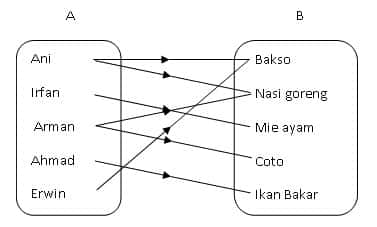
Diketahui : Ani menyukai bakso dan nasi goreng, irfan menyukai mie ayam , arman menyukai nasi gireng dan coto , ahmad menyukai ikan bakar dan erwin menyukai bakso. Buatlah kekerabatan diagram panahnya
 Demikianlah pembahasan wacana relasi, Semoga bermanfaat
Demikianlah pembahasan wacana relasi, Semoga bermanfaat
Artikel Terkait :
Sumber https://rumusrumus.com