Rumusrumus.com kali ini akan membahas ihwal rumus bidang miring beserta gambar bidang miring dan beberapa pola soalnya, lebih jelasnya simak klarifikasi dibawah ini
Pengertian Bidang Miring
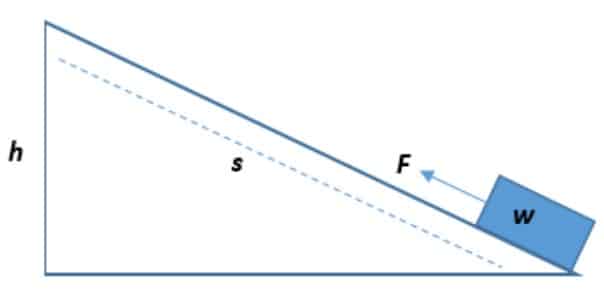
Bidang miring adalah suatu permukaan datar yang mempunyai suatu sudut, yang bukan sudut tegak lurus, terhadap permukaan horizontal.
Penerapan bidang miring sanggup mengatasi kendala besar dengan menerapkan gaya yang relatif lebih kecil melalui jarak yang lebih jauh daripada bila beban itu diangkat vertikal
Rumus Bidang Miring
Rumus bidang miring dibuat dari perpaduan antara gaya kuasa, berat benda, tinggi, dan panjang bidang miring.
Secara matematis, rumus bidang miring yaitu:
Fk x s = W x h
Keterangan Rumus :
Fk = Gaya kuasa (N)
s = Panjang bidang miring (m)
W = Berat benda (N)
h = Tinggi bidang miring (m)
Rumus Keuntungan Mekanik
W / F = s / h
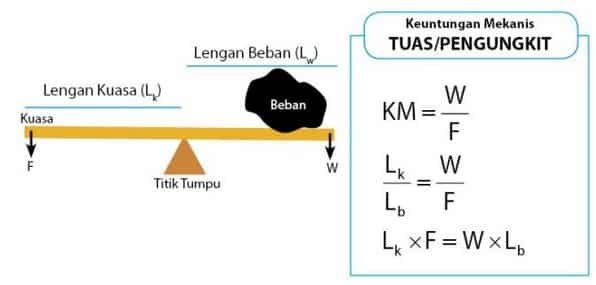
Keuntungan Mekanis Tuas
Keuntungan mekanis pesawat sederhana pertama yaitu jenis pesawat sederhana yang termasuk dalam tuas atau pengungkit. Tuas dikelompokkan menjadi 3 (tiga), pengelompokan jenis tuas ini didasarkan pada letak kuasa, titik tumpu, dan beban. Tuas jenis pertama mempunyai letak titik tumpu yang berada di tengah. Untuk tuas atau pengungkit jenis ke dua mempunyai ciri-ciri letak titik beban yang terletak di tengah. Sedangkan tuas dengan titik kuasa yang terletak di tengah dikelompokkan pada kuas jenis ke tiga.
Ada tiga titik yang terdapat pada kuas, yaitu titik tumpu, beban, dan kuasa. Jarak antara titik beban dengan titik tumpu disebut lengan beban. Sedangkan jarak antara titik kuasa dengan titik tumpu disebut lengan kuasa. Keuntungan mekanis tuas diberikan melalui persamaan di bawah ini
Contoh Alat Bidang Miring
- a. tangga naik suatu bangunan bertingkat-tingkat dan berkelok-kelok untuk memperkecil gaya
- b. jalan di pegunungan berkelok-kelok agar gampang dilalui
- c. ulir sekrup yang bentuknya ibarat tangga melingkar
- d. baji (pisau, kater, kampak, dll)
- e. dongkrak juga merupakan suatu pola bidang miring alasannya menggunakan prinsip sekrup
- f. untuk menaikkan drum keatas truk menggunakan papan kayu yang dimiringkan.
Dalam bidang miring berlaku
- a. Semakin curam suatu bidang miring, maka makin besar gaya yang diperlukan, akan tetapi jalan yang dilalui lebih pendek.
- b. Semakin landai bidang miring, maka semakin kecil gaya yang diperlukan, akan tetapi jalan yang dilalui lebih panjang.
Tujuan Bidang Miring
- Memperkecil usaha
- Mempercepat pekerjaan
- meringankan pekerjaan
Contoh Soal Bidang Miring
Contoh Soal 1.
Sebuah papan kayu digunakan untuk menurunkan sebuah drum dari truk. Tinggi truk yaitu 1,5 meter dan panjang papan 3 meter. Jika papan disandarkan pada truk, berapakah laba mekanis bidang miring tersebut?
Jawab :
s = 3 meter dan h = 1,5 meter.
Ditanya KM….?
KM = s/h
KM = 3 m / 1,5 m
KM = 2
Keunguntungan mekanis pada bidang miring yaitu 2.
Contoh Soal 2
Perhatikan gambar berikut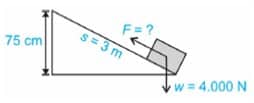
Hitunglah gaya yang dibutuhkan untuk mendorong beban pada sistem di atas!
Penyelesaian:
Diketahui :
w = 4.000 N
s = 3 m
h = 75 cm = 0,75 m
w/F = s/h
4.000 N/F = 3 m/0,75 m
4.000 N/F = 4
F = 4.000 N/4
F = 1.000 N
Contoh Soal 3
Dengan menggunakan papan yang mempunyai panjang 4 meter, pekerja mengerahkan gaya 1.250 N untuk memindahkan kotak ke langit-langit yang mempunyai tinggi 2 meter. Berapakah berat kotak itu?
Jawab :
s = 15 m
F = 1.250 N
h = 2 m
w/F = s/h
w/1250 N = 4 m/2 m
w/1250 N = 2
w = 2 . 1250 N
w = 2500 N
Contoh Soal 4
Sebuah benda mempunyai berat 1800 N akan dinaikkan ke ketinggian 2,5 m. Jika laba mekanis yang diharapkan yaitu 6, berapakah jarak yang ditempuh benda pada bidang miring dan kuasa yang dibutuhkan untuk mendorong benda tersebut?
Penyelesaian:
w = 1.800 N
h = 2,5 m
KM = 6
KM = s/h
6 = s/2,5 m
s = 6 . 2,5 m
s = 15 m
KM = w/F
6 = 1.800 N/F
F = 1.800 N/6
F = 300 N
Contoh Soal 5
Perhatikan gambar berikut
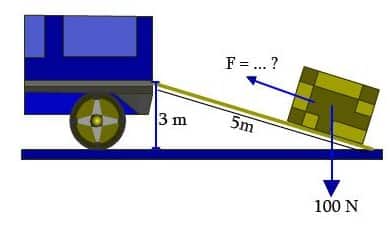
Berapakah besar gaya minimum yang dibutuhkan untuk menaikkan beban w hingga ke puncak bidang miring?
Penyelesaian:
F . s = w . h
F = (w . h)/s
F = (100 . 3)/5
F = 60 N
Maka, besarnya gaya minimum yang dibutuhkan untuk memindahkan beban hingga ke puncak bidang miring yaitu 60 N.
Demikianlah pembahasan ihwal artikel ini, Semoga bermanfaat
Rumus Terkait :
Sumber https://rumusrumus.com