Rumusrumus.com kali ini akan membahas perihal pola soal pertidaksamaan nilai mutlak, Sebelum membahas soal pertidasakaam nilai mutlak, dijelaskan terlebih dahulu perihal sifat nilai mutlak.
Tanda nilai mutlak yang disimbolkan dengan dua buah garis yang mengapit suatu persamaan. andai nilai dalam tanda mutlak lebih besar dari nol maka nilai fungsinya yakni positif. Kondisi sebaliknya juga dapat berlaku, andai nilai dalam tanda mutlak lebih kecil dari nol maka nilai fungsinya yakni negatif. namun jikalau nilai yang diberikan kedalam tanda yakni nol maka nilainya juga akan menjadi nol.
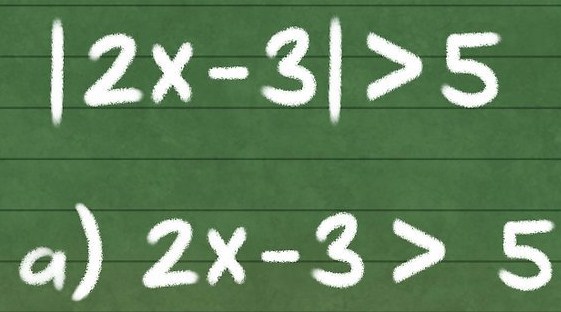
Sifat Pertidaksamaan Nilai Mutlak
Mengambil nilai mutlak dari persamaan nilai mutlak ternyata sangat mudah. Dengan mengikuti dua hukum yang penting menyerupai yang telah dibahas sebelumnya sudah dapat memilih nilai mutlaknya. Yang intinya, nilainya akan positif jikalau fungsi di dalam tanda mutlak itu lebih dari nol. Dan akan menjadi bernilai negatif andai fungsi di dalam tanda mutlaknya kurang dari nol.

Dalam pertidaksamaan nilai mutlak tak cukup dengan cara serupa. Ada pertidaksamaan aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak. Atau dapat disebut juga sebagai sifat pertidaksamaan nilai mutlak. Sifat inilah yang dapat digunakan untuk memilih himpunan penyelesaian pada soal-soal pertidaksamaan nilai mutlak yang diberikan.
Contoh Soal Pertidaksamaan Nilai Mutlak
Contoh soal 1
Tentukan interval pada penyelesaian pertidaksamaan berikut :
![]()
Jawab :
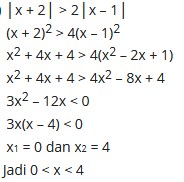
Contoh soal 2
Himpunan penyelesaian pertidaksamaan berikut ini
![]()
Jawab :
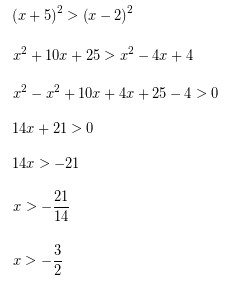
Langkah-langkah menuntaskan pertidaksamaan nilai mutlak
Pertidaksamaan nilai mutlak yakni jenis pertidaksamaan yang mengandung nilai mutlak didalamnya. Nilai mutlak menghitung jarak pada suatu angka dari 0—misalnya, |x| mengukur jarak x dari nol. Pertidaksamaan nilai mutlak dapat ditemukan dan di terapkan dalam simetri, batas-batas simetris, ataupun kondisi batas. Pahami dan selesaikan jenis-jenis pertidaksamaan ini dengan beberapa langkah yang sederhana, baik dengan cara penilaian ataupun transformasi.
Langkah 1
Evaluasi pada bentuk pertidaksamaan nilai mutlak. Seperti yang sudah disebutkan di atas, nilai mutlak x, yang dinotasikan dengan |x|, didefinisikan sebagai berikut:
Pertidaksamaan nilai mutlak umumnya mempunyai salah satu bentuk berikut:
|x| < a atau |x|> a ; |x±a| < b ataupun |x±a| > b ; |ax2+bx| < c
pada artikel ini, fokusnya yakni pertidaksamaan dengan bentuk |f(x)|< a maupun |f(x)| > a , dengan f(x) berupa fungsi apapun dan a yakni kosntanta.
Langkah 2
mengubah terlebih dahulu pertidaksamaan nilai mutlak sampai menjadi pertidaksamaan biasa. Ingat bahwa nilai mutlak dari x dapat bernilai x positif ataupun x negatif. Pertidaksamaan nilai mutlak |x| < 3 juga dapat dirubah jadi dua pertidaksamaan: -x < 3 dan x < 3.
Contoh,│x−3│>5 dapat dirubah jadi – (x-3) > 5 ataupun x-3 > 5.
|3x+2| < 5 dapat dirubah jadi – (3x+2) < 5 ataupun 3x+2 < 5.
Istilah “atau” diatas mempunyai arti bahwa kedua pertidaksamaan itu memenuhi persyaratan soal nilai mutlak
Langkah 3
Abaikan saja tanda pertidaksamaan dikala mencari nilai x untuk persamaan yang pertama. Jika membantu, ubah saja tanda pertidaksamaan jadi tanda sama dengan sampai bab tamat hanya untuk sementara.
Langkah 4
Cari nilai x menyerupai yang biasanya di lakukan. Ingat bahwa jikalau membagi dengan angka negatif untuk menyendirikan x ke salah satu sisi dari tanda pertidaksamaan, harus membalik tanda pertidaksamaannya. contohmya, jikalau membagi kedua sisi dengan -1, -x > 5 dapat menjadi x < -5.
Langkah 5
Tulis himpunan penyelesaian. Dari nilai di atas, perlu menulis jangkauan nilai yang dapat disubstitusikan ke x. Jangkauan nilai ini sering juga disebut sebagai himpunan penyelesaian. Karena harus menuntaskan dua pertidaksamaan dari pertidaksamaan nilai mutlak tersebut, maka akan mempunyai dua penyelesaian. pada pola yang digunakan di atas, penyelesaiannya dapat ditulis dengan dua cara yaitu:
-7/3 < x < 1
(-7/3,1)
Itulah langkah-langkah dan cara penyelesaian serta pola soal pertidaksamaan nilai mutlak, supaya bermanfaat
Artikel Lainya :
Sumber https://rumusrumus.com