Rumusrumus.com kali ini akan menjelaskan perihal integral yang berfokus pada pola soal integral tentu, tak tentu, substitusi, parsial, dan juga menjelaskan perihal pengertian integral termasuk integral trigonometri
Pengertian Integral
Integral merupakan bentuk pada operasi matematika yang menjadi kebalikan atau disebut invers dari operasi turunan dan limit dari jumlah ataupun suatu luas kawasan tertentu. Berdasarkan pengertian otu ada dua hal yang dilakukan dalam integral sampai dikategorikan menjadi 2 jenis integral. Yaitu, integral sebagai invers/ kebalikan dari turunan disebut juga sebagai Integral Tak Tentu. Kedua, integral sebagai limit dari jumlah ataupun suatu luas kawasan tertentu yang disebut integral tentu.
Integral Tak Tentu
Integral tak tentu dalam bahasa Inggris biasa di kenal dengan nama Indefinite Integral ataupun kadang juga di sebut Antiderivatif yang merupakan suatu bentuk operasi pengintegralan pada suatu fungsi yang menghasilkan suatu fungsi baru. Fungsi ini belum mempunyai nilai niscaya sampai cara pengintegralan yang menghasilkan fungsi tidak tentu ini disebut integral tak tentu.
Jika f berupa integral tak tentu dari suatu fungsi F maka F’= f. Proses memecahkan antiderivatif ialah antidiferensiasi Antiderivatif yang terkait dengan integral melalui “Teorema dasar kalkulus”, dan memberi cara gampang untuk menghitung integral dari banyak sekali fungsi.
Cara Membaca Integral Tak Tentu
![]()
Di baca :
Integral Tak Tentu Dari Fungsi f(x) Terhadap Variabel X
Rumus Umum Integral
![]()
Pengembangan Rumus Integral
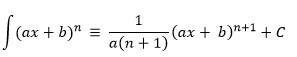
Perhatikan pola turunan dalam fungsi aljabar berikut ini:
Turunan dari fungsi aljabar y = x3 – 6 yaitu yI = 3×2
Turunan dari fungsi aljabar y = x3 + 8 yaitu yI = 3×2
Turunan dari fungsi aljabar y = x3 + 17 yaitu yI = 3×2
Turunan dari fungsi aljabar y = x3 yaitu yI = 3×2
variabel pada suatu fungsi mengalami penurunan pangkat. Berdasarkan pola itu, diketahui bergotong-royong ada banyak fungsi yang mempunyai hasil turunan yang sama yaitu yI = 3×2. Fungsi dari variabel x3 maupun fungsi dari variabel x3 yang ditambah ataupun dikurang suatu bilangan (contoh: +8, +17, atau -6) mempunyai turunan yang sama. Jika turunan itu dintegralkan, harusnya menjadi fungsi-fungsi awal sebelum diturunkan. Akan tetapi, dalam kasus tidak diketahui fungsi awal dari suatu turunan
Contoh Soal Integral
Contoh soal 1
Diketahui
![]()
Carilah integralnya ?
Jawab :
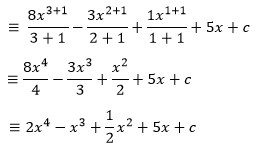
Contoh soal 2
Diketahui
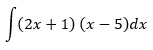
Jawab :
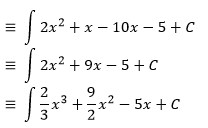
Contoh soal 3
Diketahui
![]()
Berapakah integralnya ?[
Jawab :
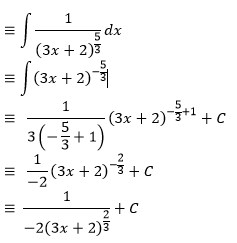
Integral Trigonometri
Integral juga bisa dioperasikan pada fungsi trigonometri. Pengoperasian integral trigonometri dilakukan dengan konsep yang sama pada integral aljabar yaitu kebalikan dari penurunan. sampai bisa disimpulkan bahwa:

Menentukan Persamaan Kurva
gradien dan persamaan garis singgung kurva di suatu titik. Jika y = f(x), gradien garis singgung kurva di sembarang titik pada kurva ialah y’ = = f'(x). Oleh alasannya yaitu itu, bila gradien garis singgungnya sudah diketahui jadi persamaan kurvanya bisa ditentukan dengan cara berikut.
y = ʃ f ‘ (x) dx = f(x) + c
Andai salah satu titik yang melalui kurva sudah diketahui, nilai c bisa diketahui sehingga persamaan kurvanya bisa ditentukan.
Contoh 1
Diketahui turunan y = f(x) ialah = f ‘(x) = 2x + 3
Andai kurva y = f(x) melalui titik (1, 6)
tentukan persamaan kurva tersebut.
Jawab :
f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.
Kurva melalui titik (1, 6), berarti f(1) = 6 hinggabisa di tentukan nilai c, yaitu 1 + 3 + c = 6 ↔ c = 2.
Maka, persamaan kurva yang dimaksud yaitu y = f(x) = x2 + 3x + 2.
Contoh 2
Gradien garis singgung kurva di titik (x, y) ialah 2x – 7. Jika kurva itu melalui titik (4, –2), tentukanlah persamaan kurvanya.
Jawab :
f ‘(x) = = 2x – 7
y = f(x) = ʃ (2x – 7) dx = x2 – 7x + c.
Karena kurva melalui titik (4, –2)
maka : f(4) = –2 ↔ 42 – 7(4) + c = –2
–12 + c = –2
c = 10
Maka, persamaan kurva tersebut yaitu y = x2 – 7x + 10.
Demikianlah pembahasan perihal integral, supaya bermanfaat
Artikel Lainya :
Sumber https://rumusrumus.com