Hasil Kali Dua Buah Vektor
Setelah mempelajari penjumlahan dua buah vektor, maka pada pembahasan kali ini kita akan mempelajari hasil kali dua buah vektor. Bagaimana caranya?
Hasil kali dua buah vektor menghasilkan dua macam hasil ialah perkalian dot (.) dan perkalian cross (x).
1. Hasil perkalian dot pada dua buah vektor
Perkalian dot (.) atau titik mempunyai hasil perkalian yang dinamakan dot product atau hasil perkalian titik (istilah dalam bahasa Indonesia). Nah, dua buah vektor yang dikali dengan perkalian titik akan menghasilkan besaran skalar. Perhatikanlah gambar berikut ini.
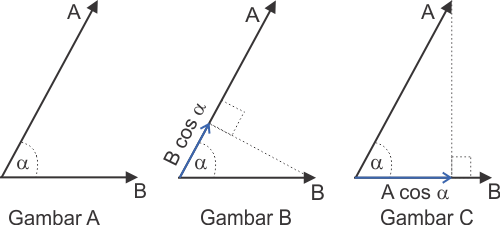
Pada gambar A di atas terdapat dua buah vektor ialah A dan B dimana kedua buah vektor tersebut pada titik pangkal O membentuk sudut sebesar α. Maka hasil perkalian titiknya atau dot product-nya ada dua macam yaitu
Perkalian A . B maknanya besar vektor A dikalikan dengan komponen vektor B yang sejajar dengan arah vektor A. Nah, perkalian ini akan menghasilkan gambar B dan persamaannya menjadi…
![]()
Perkalian B . A maknanya besar vektor B dikalikan dengan komponan besar vektor A yang sejajar dengan arah vektor B. Pada perkalian ini akan menghasilkan gambar C dan persamaannya menjadi…
![]()
2. Hasil perkalian cros pada dua buah vektor
Perkalian cros (x) atau silang mempunyai hasil perkalian yang dinamakan cross product atau hasil perkalian titik (jika diistilahkan dalam bahasa Indonesia). Jika dua buah vektor yang dikalikan dengan perkalian silang (x), maka akan menghasilkan besaran vektor baru.
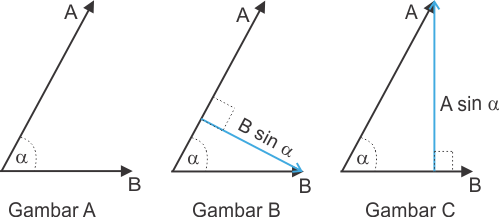
Pada gambar B mengatakan persamaan A x B=A.B sin α dimana perkalian ini mempunyai makna besar vektor A dikali dengan besar komponen vektor B yang arahnya tegak lurus terhadap arah vektor A. Sedangkan pada gambar C mengisyaratkan persamaan B x A = B.A sin α dimana perkalian ini mempunyai makna perkalian antara besar vektor B dengan besar komponen vektor A yang tegak lurus terhadap arah vektor B.
Bagaimana dengan arahnya?
Perhatikanlah gambar berikut ini.
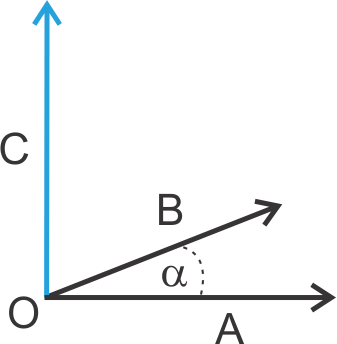
Dua buah vektor ialah A dan B mempunyai pangkal yang bertemu di titik O dimana pada pangkalnya membentuk sebuah sudut sebesar α. Maka dua buah vektor tersebut mempunyai hasil perkalian silang sebagai berikut.
![]()
Nah, besar vektor C sanggup kita peroleh melalui persamaan.
![]()
Bagaimana kalau perkaliannya dibalik? menjadi vektor B x vektor A. Jika menyerupai tu, maka akan berlaku sebaliknya ialah vektor C akan menuju arah bawah atau sumbu-y negatif. Biasanya diberi tanda minus (-).
![]()
Sehingga gambarnya menjadi menyerupai ini.
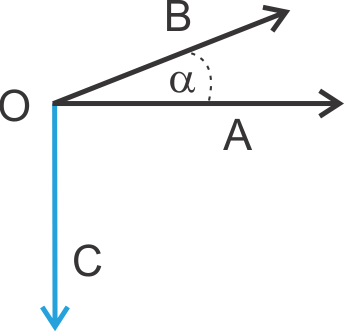
Apabila digambarkan dengan memakai koordinat kartesius, maka nanti perkalian cross akan membentuk sebuah bidang tiga dimensi yang terbentuk pada sumbu x,y dan z. Jika α = 90°, kemudian kita aplikasikan ke dalam koordinat kartesius, maka akan menjadi menyerupai ini.
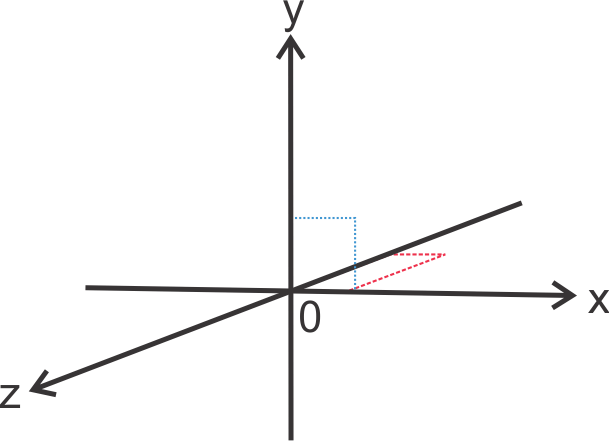
Pada gambar di atas merupakan koordinat kartesius dimana sebuah vektor yang se-arah sumbu Z merupakan hasil perkalian silang antara vektor yang searah sumbu x dengan vektor yang searah sumbu y. Ketiganya membentuk sudut siku-siku.
![]()
Dimana
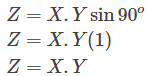
Untuk contoh-contohnya, akan kita bahas pada halaman selanjutnya. Silahkan buka halaman berjudul teladan soal dan tanggapan perkalian dua buah vektor.
Sumber https://www.siswapedia.com