Rumusrumus.com kali ini akan membahas perihal pengertian, definisi, rumus, dan teladan soal diferensial matematika beserta pembahasannya lengkap. Diferensial yaitu sebuah teori persubahaan variabel untuk lebih jelasnya simkahlah klarifikasi dibawah ini.
Pengertian Diferensial
Turunan fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f menjadi f’ yang mempunyai nilai tak beraturan. Turunan ( diferensial ) digunakan sebagai suatu alat untuk menuntaskan aneka macam problem dalam geometri dan mekanika.
Konsep turunan sebagai bab utama dari kalkulus dipikirkan pada ketika yang bersamaan oleh Sir Isaac Newton ( 1642 – 1727 ), andal matematika dan fisika bangsa Inggris dan Gottfried Wilhelm Leibniz ( 1646 – 1716 ), andal matematika bangsa Jerman.
Turunan Matematika Adalah
Misal y ialah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x
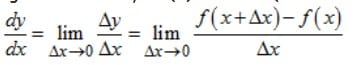
Rumus Diferensial
Rumus 1 :
Jika y = cxn dengan c dan n konstanta real
maka dy/dx = cn xn-1
contoh :
y = 2×4 maka dy/dx = 4.2×4-1 = 8×3
Rumus 2 :
Jika y = f(x) + g(x)
maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh:
y = x3 + 2×2 maka y’ = 3×2 + 4x
y = 2×5 + 6 maka y’ = 10×4 + 0 = 10×4
Rumus 3 :
Jika y = c dengan c yaitu konstanta
maka dy/dx = 0
contoh:
jika y = 6 maka turunannya yaitu sama dengan nol
Rumus 4 :
Turunan Perkalian Fungsi Jika y f(x).g(x)
maka y’ = f'(x) . g(x) + g'(x) . f(x)
contoh:
y = x2 (x2+2) maka
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
Kemudian masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4×3 + 4x (jawaban ini juga dapat diperoleh dengan cara mengalikan terlebih dahulu kemudian memakai rumus 2)
Rumus 5 :
ef (x) maka dy/dx = ef(x).f'(x)
contoh :
y = e2x+1
f (x) = 2x+1
f’ (x) = 2
maka f’ = e2x+1 . 2 = 2e2x+1
Rumus 6 :
Turunan Trigonometri Sin
Jika punya y = sin f(x)
maka turunannya yaitu y’ = cos f(x) . f'(x)
contoh :
y = sin(x2 + 1)
maka y’ = cos (x2 +1) . 2x = 2x. cos (x2 +1)
Rumus 7 :
Turunan Trigonometri Cos
Jika punya y = cos f(x)
maka turunanya adalah y’ = -sin f(x). f'(x)
contoh :
y = cos (2x+1)
maka turunannya y’ = -sin (2x+1) . 2 = -2 sin (2x+1)
Rumus Turunan Kedua
rumus turunan kedua sama dengan turunan dari turunan pertama .
Turunan kedua diperoleh dengan cara menurunkan turunan pertama.
Contoh :
Turunan kedua dari x3 + 4×2
turunan pertama = 3×2 + 8x
turunan kedua = 6x + 8
Contoh Soal Diferensial (Turunan Fungsi)
Contoh Soal 1
Persamaan garis singgung pada kurva y = 2×3-5×2-x+6 yang berabsis 1 ialah …
Penyelesaian :
y = 2×3 – 5×2 – x + 6 → x = 1
y’ = 6×2 – 10x – 1
y (1) = 2(1)3- 5(1)2 – 1 + 6
= 2 – 5 – 1 + 6
= 2 → ( 1 , 2 )
y’ = m = 6×2 – 10x – 1
= 6(1)2 – 10.1 – 1
= -5
Persamaan garis siggung : y – b = m (x – 1)
y – 2 = -5 (x – 1)
y – 2 = -5x + 1
5x + y +3 = 0
Jawaban : 5x + y + 3 = 0
Contoh Soal 2
Turunan pertama fungsi F(x) = Cos5(4x-2) ialah F’(x) = …
-5 Cos4 (4x-2) Sin (4x-2)
5 Cos4 (4x-2) Sin (4x-2)
20 Cos4 (4x-2) Sin (2x-2)
10 Cos3 (4x-2) Sin (8x-4)
-10 Cos3 (4x-2) Sin (8x-4)
Jawab :
F(x) = Cos5(4x-2)
u = Cos (4x-2) → u’ = -4Sin(4x-2)
n = 5
F’(x) = nun-1.u’
= 5 Cos5-1 (4x-2) . -4 Sin (4x-2)
= 5 Cos4 (4x-2) . -4 Sin (4x-2)
= -20 Cos4 (4x-2)Sin (4x-2)
= -10.2 Cos (4x-2)sin (4x-2) . Cos3 (4x-2)
= -10 Sin 2(4x-2) Cos3 (4x-2)
= -10 Sin (8x-4) Cos3 (4x-2)
= ( -4x+5) e-3x+4
Demikianlah Rumusrumus.com menjelaskan tentng diferensial matematika, Semoga bermanfaat
Artikel Lainya :
Sumber https://rumusrumus.com
