Pengertian Dan Metode Penyelesaian SPLDV | Metode Penyelesaian SPLDV merupakan salah satu cabang dari sistem persamaan linier. SPLDV merupakan abreviasi dari Sistem Persamaan Linier Dua Variabel. Lalu apakah yang di maksud dengan SPLDV ? Dan bagaimanakah metode penyelesaiannya ?
Apakah metode penyelesaiannya sama hal nya dengan metode penyelesaian sistem linier menyerupai yang telah kita pelajari pada pembahasan sebelumnya ? Untuk lebih terperinci lagi maka mari kita pelajari bersama kembali bagaimana metode penyelesaian sistem persamaan Linier Dua Variabel.
SPLDV
Sebelum kita mempelajari lebih mendalam perihal bagaimana metode penyelesaian sistem persamaan linier dua variabel, maka langkah pertama kita harus memahami bentuk umum spldv, pengertian, ciri – ciri dan hal – hal yang bekerjasama dengan bahan spldv (sistem persamaan linier variabel), dan nanti akan dibahas secara lengkap 4 metode spldv.
Pengertian SPLDV
SPLDV adalah suatu sistem persamaan atau bentuk korelasi sama dengan dalam bentuk aljabar yang mempunyai dua variabel dan berpangkat satu dan apabila digambarkan dalam sebuah grafik maka akan membentuk garis lurus. Dan alasannya ialah hal ini lah maka persamaan ini di sebut dengan persamaan linier.
Ciri – Ciri SPLDV
- Menggunakan korelasi tanda sama dengan ( = )
- Memiliki dua variabel
- Kedua variabel tersebut mempunyai derajat satu ( berpangkat satu )
Hal – hal Yang Berhubungan Dengan SPLDV
a. Suku
Suku yaitu bab dari suatu bentuk aljabar yang terdiri dari variabel, koefisien dan konstanta. Dan setiap suku di pisahkan dengan tanda baca penjumlahan ataupun pengurangan
Contoh :
6x – y + 4 , maka suku – suku dari persamaan tersebut ialah 6x , -y dan 4
b. Variabel
Variabel , yaitu peubah atau pengganti suatu bilangan yang biasanya dilambangkan dengan karakter menyerupai x dan y .
Contoh :
Mika mempunyai 2 buah nanas dan 5 buah jeruk.
Jika dituliskan dalam bentuk persamaan adalah
- Nanas = x
- Jeruk = y
- Persamannya ialah 2x + 5y
c. Koefisien
Koefisien yaitu suatu bilangan yang menyatakan banyaknya suatu jumlah variabel yang sejenis. Koefisien disebut juga dengan bilangan yang ada di depan variabel, alasannya ialah penulisan sebuah persamaan koefifien berada di depan variabel
Contoh :
Mika mempunyai 2 buah nanas dan 5 buah jeruk. Jika di tulis dalam bentuk persamaan ialah :
Jawab :
- Nanas = x dan Jeruk = y
- Persamannya ialah 2x + 5y
- Dimana 2 dan 5 ialah koefisien. Dan 2 ialah koefisien x dan 5 ialah koefisien y
d. Konstanta
Konstanta yaitu bilangan yang tidak diikuti dengan variabel, maka nilainya tetap atau konstan untuk berapapun nilai perubahnya
Contoh :
2x + 5y + 7 , dari persamaan tersebut konstanta ialah 7 , alasannya ialah 7 nilainya tetap dan tidak terpengaruh dengan berapapun variabelnya
Itulah beberapa hal yang bekerjasama perihal bentuk umum spldv untuk kita pahami sebelum kita memahami perihal rumus spldv.
Syarat Sistem Persamaan Linier Dua Variabel sanggup mempunyai satu penyelesaian, yaitu :
- Ada lebih dari satu atau ada dua persamaan linier dua variabel sejenis
- Persamaan linier dua variabel yang membentuk sistem persamaan linier dua variabel, bukan persamaan linier dua variabel yang sama
Jadi kedua syarat ini wajib sanggup terpenuhi sebelum kita menghitung persamaan linier dua variabel.
Metode Penyelesaian Sistem Persamaan Linier Dua Variabel
Untuk menuntaskan cara menghitung spldv (sistem persamaan linier dua variabel) maka sanggup diselesaikan dengan 4 metode berikut ini :
- Metode Substitusi
- Metode Eliminasi
- Metode Gabungan (Subsitusi dan Eliminasi)
- Metode Grafik
Untuk lebih terperinci perihal ke-4 metode diatas disini RumusRumus.com akan membahas secara lengkap metode penyelesaian spldv beserta teladan soal spldv dan pembahasannya.
1. Metode Substitusi atau Metode Mengganti
Metode substitusi, yaitu metode atau cara menuntaskan SPLDV dengan mengganti salah satu peubah atau variabel.
Berikut ini langkah – langkah untuk menuntaskan spldv memakai metode Substitusi :
- Ubahlah salah satu dari persamaan menjadi bentuk x = cy + d atau y = ax + b
- a, b, c, dan d ialah nilai yang ada pada persamaan
- Triknya kalian harus mencari dari 2 persamaan carilah salah satu persamaan yang termudah
- Setelah mendapat persamaannya substitusi kan nilai x atau y
- Selesaikan persamaan sehingga mendapat nilai x ataupun y
- Dapatkan nilai variabel yang belum diketahui dengan hasil langkah sebelumnya
Contoh Soal Spldv Dengan Metode Substitusi
Contoh Soal 1
1. Tentukan Himpunan penyelesaian dari persamaan berikut ini x + 3y = 15 dan 3x + 6y = 30
Penyelesaian :
Diketahui :
Persamaan Pertama = x + 3y = 15
Persamaan Kedua = 3x + 6y = 30
Langkah Pertama : Ubah salah satu persamaan, carilah yang termudah
x + 3y = 15 —> x = -3y + 15
Langkah Kedua : Subsititusi nilai x = -3y + 15 ke dalam persamaan kedua untuk mencari nilai y , maka akibatnya sebagai berikut :
3x + 6y = 30
3 ( -3y +15 ) + 6y = 30
-9y + 45 + 6y = 30
-3y = 30 – 45
-3y = -15
y = 5
Langkah Ketiga : Selanjutnya untuk mencari nilai x maka, gunakan salah satu persamaan boleh persamaan pertama atau kedua :
Dari Persamaan Pertama :
+ 3y = 15
x + 3 ( 5 ) = 15
x + 15 = 15
x = 0
Dari Persamaan Kedua :
3x + 6y = 30
3x + 6 ( 5 ) = 30
3x + 30 = 30
3x = 0
x = 0
Langkah Keempat : Maka nilai Kaprikornus HP = { 0 , 5 }
Contoh Soal 2
2. Tentukan Penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , kalau x = a dan y = b . Maka tentukan nilai a dan b !
Penyelesaian :
Diketahui :
Persamaan Pertama = 3x+ 5y = 16
Persamaan Kedua = 4x + y = 10
Langkah Pertama : Ubah salah satu persamaan, carilah yang termudah
4x + y = 10 —> y = -4x + 10
Langkah Kedua : Subsititusi nilai 4x + y = 10 ke dalam persamaan kedua untuk mencari nilai x , maka akibatnya sebagai berikut :
3x + 5y = 16
3x + 5 ( -4x + 10 ) = 16
3x – 20x + 50 = 16
-17x = 16 – 50
-17x = -34
x = 2
Langkah Ketiga : Selanjutnya untuk mencari nilai y maka, gunakan salah satu persamaan boleh persamaan pertama atau kedua :
Dari Persamaan Pertama :
3x + 5y = 16
3(2) + 5y = 16
6 +5y = 16
5y = 16 – 6
5y = 10
y = 2
Dari Persamaan Kedua :
4x + y = 10
4(2) + y = 10
8 +y = 10
y = 2
Langkah Keempat : Maka, kita ketahui nilai x = 2 dan nilai y = 2 . Dan Yang ditanyakan ialah nilai a dan b , dimana x = a dan y = b , maka :
x = a = 2
y = b = 2
2. Metode Eliminasi atau Metode Menghilangkan
Langkah – langkah menuntaskan spldv dengan metode eliminasi :
- Metode eliminasi ialah Metode atau cara untuk menuntaskan sistem persamaan linier dua variabel dengan cara mengeliminasi atau menghilngkan salah satu peubah (variabel) dengan menyamakan koefisien dari persamaan tersebut.
- Cara untuk menghilangkan salah satu peubahnya yaitu dengan cara perhatikan tandanya, apabila tandanya sama [(+) dengan (+) atau (-) dengan (-) ] , maka untuk mengeliminasinya dengan cara mengurangkan. Dan sebaliknya apabila tandanya berbeda maka gunakanlah sistem penjumlahan.
Untuk lebih jelasnya perihal langkah – langkah diatas maka perhatikan teladan soal spldv eliminasi di bawah ini :
Contoh Soal SPLDV Eliminasi 1
1. Tentukan Himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30
Penyelesaian :
Diketahui :
Persamaan 1 = x + 3y = 15
Persamaan 2 = 3x + 6y = 30
Langkah Pertama yaitu memilih variabel mana yang akan di eliminasi terlebih dahulu. Kali ini kita akan menghilangkan x terlebih dahulu, dan biar kita temukan nilai y . Caranya yaitu :
3x + 6y = 30 : 3
x + 2y = 10 . . . . ( 1 )
x + 3y = 15 . . . .(2)
Langkah Kedua Dari persamaan (1) dan (2), mari kita eliminasi, sehingga akibatnya :
x + 3y = 15
x + 2y = 10 _
y = 5
Langkah Ketiga Selanjutnya, untuk mengetahui nilai x , maka caranya sebagai berikut :
x + 3y = 15 | x2 | <=> 2x + 6y = 30 . . . .( 3 )
3x + 6y = 30 | x1 | <=> 3x + 6y = 30 . . .. (4 )
Eliminasi antara persamaan (3) dengan (4 ), yang akibatnya menjadi :
3x + 6y = 30
2x + 6y = 30 _
x = 0
Maka, Himpunan penyelesaiannya ialah HP = { 0 . 5 }
Contoh Soal SPLDV Eliminasi 2
2. Tentukan Penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , kalau x = a dan y = b . Maka tentukan nilai a dan b !
Penyelesaian :
Diketahui :
Persamaan 1 = 3x+ 5y = 16
Persamaan 2 = 4x + y = 10
Langkah Pertama yaitu tentukan variabel mana yang akan di eliminasi terlebih dahulu perhatikan penyelesaian di bawah ini :
3x+ 5y = 16 | x1 | <=> 3x + 5y = 16 . . . .( 1 )
4x + y = 10 | x5 | <=> 20x + 5y = 50 . . . ( 2 )
Dari persamaan (1 ) dan (2 ), sanggup kita eliminasi dan menghasilkan :
20x + 5y = 50
3x + 5y = 16 _
17 x + 0 = 34
x = 34 / 17
x = 2
Langkah Kedua Selanjutnya, lakukan langkah yang sama namun kali ini yang harus sama x nya , maka caranya ialah :
3x+ 5y = 16 | x4 | <= > 12 x + 20y = 64 . . .(3)
4x + y = 10 | x3 | <=> 12x + 3y = 30 . . . .(4)
Langkah Ketiga Persamaan (3) dan (4) , mari kita eliminasi untuk menghasilkan nilai y :
12 x + 20y = 64
12x + 3y = 30 _
0 + 17y = 34
y = 2
Jadi , HP ={ 2 ,2 } , dan nilai a dan b ialah :
a= x = 2 dan b = y = 2
3. Metode Campuran (Eiminasi dan Substitusi) Atau Gabungan
Metode adonan atau biasa disebut juga dengan metode gabungan, yaitu suatu cara atau metode untuk menuntaskan suatu persamaan linier dengan mengunakan dua metode yaitu metode eliminasi dan substitusi secara bersamaan.
Karena pada masing – masing metode mempunyai keunggulan masing – masing diantaranya ialah :
- Metode Eliminasi mempunyai keunggulan baik di awal penyelesaian.
- Metode substitusi mempunyai keunggulan baik diakhir penyelesaian.
- Maka dengan menggabungkan ke-2 metode ini akan mempermudah dalam meneyelasikan spldv
Untuk lebih terperinci perihal penggunaan metode gabungan / adonan spldv ini maka silahkan perhatikan teladan soal spldv gabungan dibawah ini :
Contoh Soal SPLDV Metode Gabungan
1. Diketahui persamaan x + 3y = 15 dan 3x + 6y = 30, dengan memakai metode adonan tentukanlah Himpunan penyelesaiannya !
Penyelesaian :
Diketahui :
Persamaan 1 = x + 3y = 15
Persamaan 2 = 3x + 6y = 30
Langkah Pertama Menggunakan Metode Eliminasi :
x + 3y = 15 | x3| <=> 3x +9x = 45
3x + 6y = 30 | x1| <=> 3x + 6y = 30 _
0 + 3y = 15
y = 5
Langkah Kedua Menggunakan Metode Substusi :
x + 3y = 15
x + 3.5 = 15
x + 15 = 15
x = 0
Jadi himpunan penyelesaian dari soal diatas adalah HP ={ 0 , 5 }
4. Metode Grafik
Metode sistem persamaan linear dua variabel yang ke-empat ini ialah metode grafik. Berikut ini langkah-langkah untuk menuntaskan SPLDV dengan metode grafik sebagai berikut :
Langkah – langkah menuntaskan SPLDV dengan metode grafik :Langkah Pertama :
- Tentukan nilai koordinat titik potong masing-masing persamaan terhadap sumbu-X dan juga sumbu-Y
- Gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius
Langkah Kedua :
- Jika kedua garis pada grafik berpotongan pada satu titik, maka himpunan penyelesaiannya mempunyai satu anggota.
- Jika kedua garis sejajar, maka himpunan penyelesaiannya tidak mempunyai anggota. Maka sanggup dikatakan himpunan penyelesaiannya ialah himpunan kosong, dan sanggup ditulis ∅.
- Jika kedua garis saling berhimpit, maka himpunan penyelesaiannya mempunyai anggota yang tak terhingga
Dari klarifikasi kedua langkah diatas maka banyak anggota dari himpunan spldv sebagai berikut :
a1x + b1y = c1
a2x + b2y = c2
Agar lebih memahami perihal metode grafik spldv silahkan lihat teladan soal dan pembahasan dibawah ini :
Contoh Soal Spldv Metode Grafik
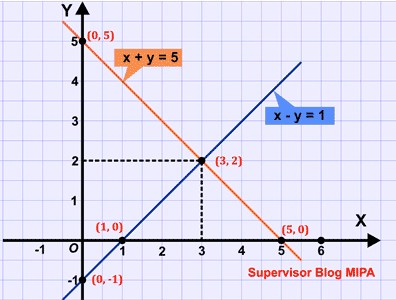
1. Tentukan himpunan penyelesaian dari persamaan berikut ini :
Persamaan 1 : x + y = 5
Persamaan 2 : x − y = 1
Penyelesaian :
Langkah Pertama, Tentukan titik potong sumbu-x dan sumbu-y
Titik Potong untuk Persamaan 1 yaitu x + y = 5
Menentukan titik potong sumbu-x maka syaratnya y = 0
x + y = 5
x + 0 = 5
x = 5
Maka titik potong nya (5,0)
Menentukan titik potong sumbu-y maka syaratnya x = 0
x + y = 5
0 + y = 5
y = 5
Maka titik potong nya (0,5)
Titik Potong untuk Persamaan 2 yaitu x – y = 1
Menentukan titik potong sumbu-x maka syaratnya y = 0
x – y = 1
x – 0 = 1
x = 1
Maka titik potong nya (1,0)
Menentukan titik potong sumbu-y maka syaratnya x = 0
x – y = 1
0 – y = 1
y = -1
Maka titik potong nya (0,-1)
Langkah Kedua, Gambarkan grafik dari masing – masing titik potong dari kedua persamaan diatas. Maka akibatnya sanggup dilihat digambar dibawah ini :
Dilihat dari gambar grafik di atas, maka titik potong dari kedua grafik diatas ialah di titik (3, 2)
Maka hasil dari Himpunan Penyelesaian ialah {3,2}
Kesimpulan :
Demikian klarifikasi mengenai Metode penyelesaian SPLDV . Praktis bukan ? prinsipnya sama dengan cara menuntaskan persamaan linier. Dan yang perlu dipahami benar yaitu bentuk sisitem persamaan linier dua variabel itu menyerupai apa. Kata kuncinya ialah dua variabel , berarti peubahnya ada dua yaitu x dan y atau simbol yang lainnya.
Dan diantara cara kempat di atas, cara nomor tigalah yang paling efektif dan efisien. Kenapa demikian ? alasannya ialah juga kita sedang menuntaskan Soal UAS , niscaya menjadi mempercepat waktu dan yang penting hasilnyapun benar.
Semoga dengan klarifikasi di atas sedikit banyak sanggup membantu menuntaskan masalah sistem persamaan linier dua variabel, Semoga Bermanfaat ….
Artikel Terkait :
Sumber https://rumusrumus.com