RumusRumus.com – kali ini akan membahas wacana rumus himpunan yang mencakup pengertian himpunan dan juga rumus himpunan beserta klarifikasi dari jenis himpunan, irisan himpunan, cara menyatakan himpunan dan himpunan penyelesaian (SPLDV). Untuk lebih jelasnya simak pembahasan dibawah ini
Pengertian Himpunan
Himpunan adalah kumpulan benda atau objek yang sanggup didefinisikan dengan jelas, sampai dengan sempurna sanggup diketahui objek yang termasuk himpunan dan yang tidak termasuk dalam himpunan tersebut.
Suatu himpunan dilambangkan dengan abjad kapital A, B, C, D, E, …………….. Z, benda ataupun objek yang termasuk kedalam himpunan disebut anggota himpunan atau elemen himpunan ditulis dengan sepasang kurung kurawal {……..}
Jenis Jenis Himpunan
1. Himpunan Semesta
Himpunan semesta atau semesta pembicaraan yaitu himpunan yang memuat semua anggota ataupun objek himpunan yang dibicarakan.
Himpunan semesta (semesta pembicaraan) umumnya dilambangkan dengan S atau U.
Contoh: Kalau kita membahas mengenai 1, ½, -2, -½,… maka semesta pembicaraan kita yaitu bilangan real.
Jadi himpunan semesta yang dimaksud yaitu R. Apakah hanya R saja? Jawabannya tidak. Tergantung kita mau membatasi pembicaraanya.
Pada rujukan di atas sanggup saja dikatakan semestanya yaitu C (himpunan bilangan kompleks). Namun kita dihentikan mengambil Z (himpunan bilangan bulat) sebagai semesta pembicaraan.
2. Himpunan Kosong
Himpunan kosong yaitu himpunan yang tidak memiliki anggota, dan dinotasikan dengan {} atau ∅. Himpunan nol yaitu himpunan yang hanya memiliki l anggota, yaitu nol (0).
3. Himpunan Bagian
Himpunan A merupakan himpunan bab B, bila setiap anggota A juga menjadi anggota B dan dinotasikan A ⊂ B atau B ⊃ A.
Jika ada himpunan A dan B di mana setiap anggota A merupakan anggota B, maka dikatakan A merupakan himpunan bab (subset) dari B atau dikatakan B memuat A dan dilambangkan dengan A ⊂ B.
Jadi, A ⊂ B bila dan hanya bila 𝑥 ⊂ A ⇒ 𝑥 ⊂ B
Jika ada anggota dari A yang bukan merupakan anggota B, maka A bukan bukan himpunan bab dari B, dilambangkan dengan A ⊄ B.
Cara Menyatakan Himpunan
Himpunan sanggup dinyatakan melalui tiga cara :
- Dengan kata-kata
yaitu dengan menyebutkan semua syarat ataupun sifat-sifat keanggotaan dari suatu himpunan.
Contoh: A yaitu himpunan bilangan orisinil antara 5 dan 12, ditulis A = {bilangan orisinil antara 5 dan 12} - Dengan Notasi Pembentuk Himpunan
yaitu menyebutkan semua syarat atau sifat ke-anggotaan dari suatu himpunan, namun anggota himpunan dinyatakan dalam variabel peubah.
Contoh: A yaitu himpunan bilangan orisinil antara 5 dan 12, dituliskan {x: 5<x<12,x bilangan asli}. - Dengan Mendaftar Anggota-anggotanya
Yaitu menuliskan anggota-anggota himpunan dalam pasangan kurung kurawal dan memisahkan dengan tanda koma.
Contoh: A yaitu himpunan bilangan orisinil antara 5 dan 12, ditulis A= {6,7,8,9,10,11}
Operasi Himpunan
1. Irisan Himpunan
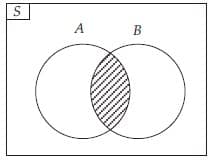
Irisan dari dua himpunan A dan B yaitu himpunan yang anggota-anggotanya ada di himpunan A dan ada di himpunan B. Dengan kata lain yaitu himpunan yang anggotanya ada di kedua himpunan tersebut.
Contoh: A = {a, b, c, d, e} dan B = {b, c, f, g, h}
Pada kedua himpunan tersebut ada dua anggota yang sama yaitu b dan c. Oleh lantaran itu, sanggup dikatakan bahwa irisan himpunan A dan B yaitu b dan c atau ditulis dengan:
A ∩ B = {b, c}
A ∩ B dibaca himpunan A irisan himpunan B. Dengan diagram Venn A ∩ B sanggup dinyatakan ibarat pada Gambar berikut ini.
2. Gabungan Himpunan
A gabungan B ditulis A ∪ B = {x | x ∈ A atau x ∈ B}
Contohnya :
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ∪ B = {1, 2, 3, 4, 5, 7, 11}
3. Selisih
A Selisih B ditulis A-B = {x | x ∈ A atau x Ï B}
Contohnya :
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A-B = {1, 4}
4. Komplemen himpunan
Komplemen A ditulis A1 atau Ac = {x | x ∈ S dan x Ï A}
Contohnya :
A= {1, 2, … , 5}
S = {biangan Asli kurang dari 10}
Ac = {6, 7, 8, 9}
Contoh Soal operasi himpunan
Jika Diketahui: A= {1, 2, 3, 4, 5}
B = {2, 3, 6, 7, 8}
C = {4, 5, 6, 7, 8}
Tentukanlah:
a. A ∩ B c. B ∩ C
b. A ∩ C d. A ∩ B ∩ C
Jawab :
a. A ∩ B = {2, 3} c. B ∩ C = {6, 7, 8}
b. A ∩ C = {4, 5} d. A ∩ B ∩ C = { }
Diagram Venn
Diagram venn yaitu menyajikan suatu himpunan dengan satu himpunan menggunakan lingkaran dan seluruh himpunan atau himpunan semesta digambarkan dengan gambar segi empat.
Macam – Macam Himpunan
- Himpunan bilangan asli, yaitu A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, … }
- Himpunan dari bilangan cacah , yaitu C = { 0, 1, 2, 3, 4, 5, 6, 7, …. }
- Himpunan dari bilangan prima, yaitu X = { 2, 3, 5, 7, …. }
- Himpunan bilangan ganjil, yaitu G = { 1, 3, 5, 7, 9, 11, 13, 15, …. }
- Himpunan bilangan genap, contohnya G = { 0, 2, 4, 6, 8, 10, 12, 14, 16, …. }
- Dan seterusnya.
Himpunan Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)
Untuk memilih himpunan penyelesaian dari sistem persamaan linear dua variabel sanggup dilakukan dengan empat metode yaitu :
- metode grafik
- metode substitusi
- metode eliminasi
- metode adonan (substitusi dan eliminasi).
Jika ada dua buah persamaan liniear dua variabel berbentuk ax + by = c dan px + qy = r, dimana persamaan yang satu dan lainnya tidak terpisahkan, maka persamaan-persamaan itu dinamakan sistem persamaan linear dua variabel.
Bentuk umum sistem persamaan linear dua variabel yaitu:
ax + by = c
px + qy = r
Pada sistem persamaan linear dua variabel (SPLDV) a, b, p, dan q disebut koefisien, x dan y ialah variabel dari SPLDV, serta c dan r disebut konstanta.
Metode Grafik
Ketika menggunakan metode grafik, wajib menggambar masing-masing persamaan linear dua variabel dalam koordinat kartesius. Himpunan penyelesaiannya yaitu titik potong dari kedua garis.
Jika garisnya tidak berpotongan atau sejajar, Maka himpunan penyelesaiannya yaitu himpunan kosong. Tetapi bila garisnya berhimpit maka jumlah himpunan penyelesaiannya tak berhingga.
Metode Subtitusi
Langkah-langkah dengan menggunakan metode substitusi untuk mencari himpunan penyelesaian dari SPLDV yaitu sebagai berikut.
- Ubahlah salah satu persamaan ke dalam bentuk x = … atau y = …
- Masukkan (substitusi) nilai x atau y yang di sanggup ke dalam persamaan yang kedua
- Nilai x atau y yang di sanggup kemudian kemudian disubstitusikan ke dalam salah satu persamaan untuk memperoleh nilai variabel lainnya yang belum diketahui (x atau y).
Metode Eliminasi
Penyelesaian SPLDV dengan metode eliminasi intinya yaitu menghilangkan (mengeliminasi) salah satu variabel dari sistem persamaan yang akan dicari himpunan penyelesaiannya.
Caranya dengan menjumlahkan ataupun mengurangkan kedua sistem persamaan tersebut.
Untuk memilih variabel y, maka hilangkan terlebih dahulu variabel x.
Begitu juga sebaliknya, untuk memilih variabel x, maka hilangkan terlebih dahulu variabel y.
Sebagai catatan
Untuk menghilangkan variabel x atau y maka koefisien dari masing-masing variabel dalam sistem persamaan harus sama.Jika salah satunya tidak sama maka harus disamakan terlebih dahulu. Caranya mengalikan dengan bilangan bundar tertentu sehingga koefisiennya menjadi sama
Metode Campuran (Eliminasi dan Substitusi)
Dalam pengerjaan soal persamaan linear dua variabel, terkadang menemukan kesulitan bila menggunakan metoda eliminasi untuk memilih himpunan penyelesaiannya.
Oleh alasannya itu, sanggup menggunakan metode campuran, yaitu dengan cara memilih salah satu variabel x atau y dengan menggunakan metode eliminasi.
Hasil yang diperoleh dari x atau y kemudian disubstitusikan ke salah satu persamaan linear dua variabel tersebut.
Demikianlah pembahasan wacana bahan himpunan, Semoga bermanfaat
Baca Juga :
Sumber https://rumusrumus.com