Rumusrumus.com kali ini akan membahas ihwal interpolasi yang mencakup rumus dari banyak sekali macam interpolasi dan beberapa pola soal interpolasi beserta jawabannya.
Pengertian Interpolasi
Interpolasi ialah proses pencarian dan penghitungan pada nilai suatu fungsi yang grafiknya melewati sekumpulan titk yang diberikan. Titik-titik itu mungkin merupakan hasil eksperimen pada sebuah percobaan, ataupun didapat dari suatu fungsi yang diketahui
Interpolasi Perbandingan Segitiga
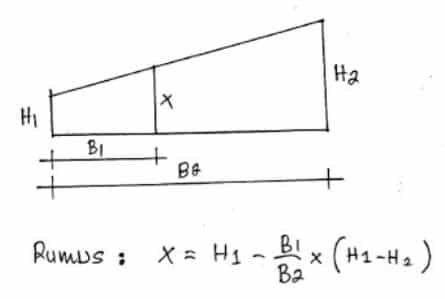
Contoh :
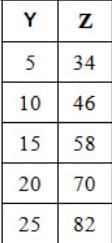
Jika Y = 17, berapakah nilai Z ?
Penyelesaian :
Nilai Y = 17 itu artinya range didapatkan antara 15 sampai 20
dari tabel didapatkan:
H1=58
H2=70
B1=20-17=3
B2=20-15=5
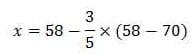
nilai x didapat = 65,20
Interpolasi Linear
Interpolasi linear adalah cara mendapat nilai di antara dua data yang menurut persamaan linear. Interpolasi linier merupakan metoda untuk penentuan suatu nilai fungsi persamaan linear menurut aturan kesebandingan.
Rumus Interpolasi Liniear
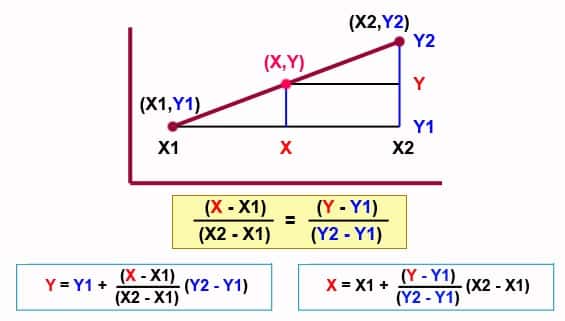
Contoh Cara Melakukan Interpolasi Linear
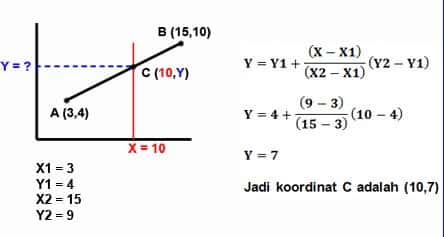
Soal: Diketahui pada sebuah garis lurus yang melewati koordinat titik A (3,4) dan koordinat titik B (15,10) pada suatu sistem koordinat X dan Y. Garis AB berpotongan dengan garis vertikal dengan persamaan X = 9 di titik C. Tentukanlah koordinat titik C.
Jawaban :
X1 = 3
Y1 = 4
X2 = 15
Y2 = 10
X = 9
Interpolasi Dalam Statistika
Contoh:
Jika sebuah penelitian memiliki jumlah sampel 60 responden dengan derajat kebebasan yaitu n-2=58.
Dalam tabel t, begitu sulit untuk mengkonsultasi nilai d.k sebesar 58 tersebut alasannya ialah nilai 58 tidak dituliskan secara konkret akan tetapi berada diantara d.k. 40 dan d.k. 60 sampai perlu dilakukan nilai 58 dalam tabel tersebut.
Perhitungan interpolasi tersebut dilakukan dengan menggunakan rumus dibawah:
Rumus Interpolasi Dalam Statistika
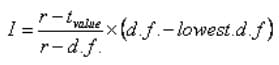
Keterangan Rumus :
I = nilai interpolasi
r-tvalue = range (selisih) nilai t pada tabel dari dua d.k. yang terdekat
Untuk pola diatas nilai d.k. 58 berada pada d.k. 40 dan d.k. 60, nilai t untuk d.k. 40 pada tabel ialah 1,684 sedangkan nilai t untuk d.k. 60 yaitu 1,671.
Maka selisih nilai t yaitu 1,684 – 1,671 = 0,013
r-d.f. = range (selisih) dari dua d.k. yang terdekat
Selisih dari nilai dua d.k. terdekat ialah 60 -40 = 20
Lalu nilai interpolar itu dimasukkan sebagai nilai pengurang dari nilai t untuk d.k terdekat yang paling rendah. Hasil inilah yang lalu digunakan sebagai nilai t untuk d.k. yang tidak tercantum dalam tabel.
Maka Perhitungannya yaitu :
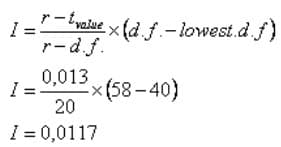
Nilai t untuk d.k. 58 = nilai t untuk d.k. 40 – I
= 1,684 – 0,0117
= 1,6723
Interpolasi Kuadratik
Interpolasi Kuadratik digunakan untuk mencari titik-titik antara dari 3 buah titik
P1(x1,y1), P2(x2,y2) dan P3(x3,y3) dengan menggunakan pendekatan fungsi kuadrat
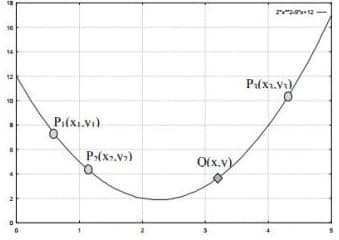
Untuk mendapat titik Q(x,y) digunakan interpolasi kuadratik sebagai berikut:
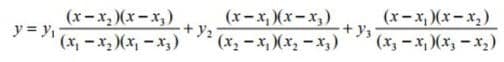
Interpolasi Polinomial
Interpolasi polynomial digunakan untuk mencari titik-titik antara dari n buah titik P1(x1,y1), P2(x2,y2), P3(x3,y3), …, PN(xN,yN) dengan menggunakan pendekatan fungsi polynomial pangkat n-1:
![]()
Masukkan nilai dari setiap titik ke dalam persamaan polynomial di atas dan didapat persamaan simultan dengan n persamaan dan n variable bebas:
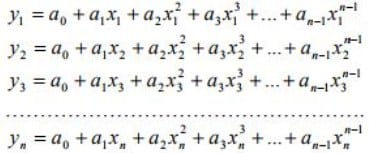
Penyelesaian persamaan simultan di atas yaitu nilai-nilai a0, a1, a2, a3, …, an yang
merupakan nilai-nilai koefisien dari fungsi pendekatan polynomial yang akan dipakai. Dengan memasukkan nilai x dari titik yang dicari pada fungsi polinomialnya, akan diperoleh nilai y dari titik tersebut.
Demikianlah klarifikasi ihwal interpolasi, Semoga bermanfaat
Materi Terkait :
Sumber https://rumusrumus.com