√ Memahami Macam – Macam Teladan Bilangan Dalam Matematika

Macam – macam referensi bilangan | Pola bilangan merupakan sub penggalan dari bahan barisan bilangan atau penggalan yang perlu di fahami terlebih dahulu sebelum melanjut pada bahan barisan aritmatika dan barisan geometri .Pola bilangan juga merupakan bahan yang tidak kalah penting untuk dipelajari .

Pola bilangan sendiri mempunyai arti suatu susunan bilangan yang mempunyai bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu referensi . Dan referensi bilanga juga mempunyai banyak jenisnya atau macamnya . Pada kesempatan kali ini , kita akan mempelajarinya bersama .

Macam – macam Pola Bilangan

Macam – macam referensi bilngan mencakup beberapa jenis berikut ini :

1. Pola Bilangan Ganjil 

Poal bilangan ganjil yaitu referensi bilangan yang terbentuk dari bilangan – bilangan ganjil . Sedangkan pengertian dari bilangan ganjil sendiri mempunyai arti suatu bilangan orisinil yang tidak habis dibagi dua ataupun kelipatannya .

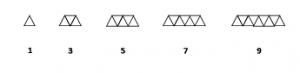
• pola bilangan ganjil yaitu :  1 , 3 , 5 , 7 , 9 , . . . .


• Gambar Pola bilangan ganjil :

• Rumus Pola Bilangan ganjil

1 , 3 , 5 , 7 , . . . , n , maka rumus referensi bilangan ganjil ke n adalah :

Un = 2n – 1 

Contoh :

1 , 3 , 5 , 7 , . . . , ke 10

Berapakah referensi bilangan ganjil ke 10 ?

Jawab :

Un = 2n – 1

U10 = 2 . 10 – 1

        = 20 – 1   = 19

2. Pola Bilangan Genap 

pola bilangan genap yaitu referensi bilangan yang terbentuk dari bilangan – bilangan genap . Bilangan genap yaitu bilangan orisinil yaitu bilangan orisinil yang habis dibagi dua atau kelipatannya .

• Pola bilangan genap yaitu : 2 , 4 , 6 , 8 , . . .


• Gambar referensi bilangan genap :

• Rumus Pola bilangan genap

2 , 4 , 6 , 8 , . . . . , n  maka rumus referensi bilangan genap ke n yaitu : 

Un = 2n 

Contoh :

2 , 4 , 6 , 8 , . . . ke 10 .berapakah referensi bilangan genap ke 10 ?

jawab :

Un = 2n

U10 = 2 x 10

        = 20

3. Pola bilangan Persegi 

Pola bilangan persegi , yaitu suatu barisan bilangan yang membentuk suatu referensi persegi .

• Pola bilangan persegi yaitu 1 , 4 , 9 , 16 , 25 ,  . . .


• Gambar Pola bilangan persegi :

• Rumus Pola bilangan persegi

1 , 4 , 9 , 16 , 25 , 36 , . . . , n  maka rumus untuk mencari referensi bilangan persegi ke n yaitu :

Un =  n²

Contoh :

Dari suatu barisan bilangan 1 , 2 , 9 , 16 , 25 , 36 , . . . ,ke 10 . Berapakah referensi bilangan ke 10 dalam referensi bilangan persegi ?

Jawab :

Un = n²

U10 = 10²     = 100

4. Pola Bilangan Persegi Panjang 

Pola bilangan persegi panjang yaitu suatu barisan bilangan yang membentuk referensi persegi panjang .

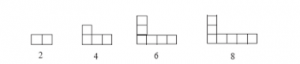
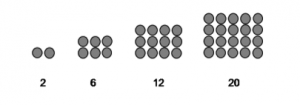
• Pola persegi panjang yaitu 2 , 6 , 12 , 20 , 30 , . . .


• Gambar Pola Bilangan persegi panjang :

• Rumus referensi bilangan persegi panjang

2 , 6 , 12 , 20 , 30 , . . .  n  , maka Rumus Pola bilangan Persegi panjang ke n yaitu :

Un = n . n + 1 

Contoh :

Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 10 . Berapakah referensi bilangan persegi ke 10 ?

Jawab :

Un = n . n+ 1

U10 = 10 . 10 + 1

        = 10 . 11

       = 110

5. Pola Bilangan Segitiga 

Pola bilangan segitiga yaitu suatu barisan bilangan yang membentuk sebuah referensi bilangan segitiga .

• Pola bilangan segitiga yaitu : 1 , 3 , 6 , 10 , 15 , . . .


• Gambar Pola bilangan segitiga :

• Rumus Pola Bilangan Segitiga :

1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus referensi bilangan segitiga ke n yaitu : 

Un = 1 / 2 n ( n + 1 ) 

Contoh Soal :

Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 10 . Berapakah referensi bilangan segitiga ke 10 ?

Jawab :

Un = 1/2 n ( n + 1 )

U 10 = 1/2 .10 ( 10 + 1 )

         = 5 ( 11 )  = 55

6. Pola Bilangan FIBONACCI 

Pola bilangan fibonacci yaitu suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depanya .

• Pola bilangan fibonacci :

1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 56 , . . .

2 , 2 , 4 , 6 , 10 , 16 , 26 , 42 , . . ..

Demikian klarifikasi mengenai pola bilangan dalam ilmu matematika . Pada dasarnya , referensi bilangan merupakan suatu bentuk barisan bilangan . Apabila kita dalam memperhatikanya tidak terlalu cermat, maka referensi yang satu dengan referensi bilangan yang lain tidak ada bedanya . Namun , referensi bilangan mempunyai fungsi yang sangat besar yaitu semoga lebih gampang dalam mengerjakan barisan aritmatika dan geometri . Semoga bermanfaat . . .

Sumber https://rumusrumus.com

√ Barisan Bilangan Aritmatika Dan Geometri

Barisan Bilangan  | Barisan bilangan merupakan salah satu bentuk cabang ilmu matematika yang merupakan bentuk bahan  kelanjutan dari contoh bilangan yang telah kita pelajari pada pembahasan sebelumnya . Barisan bilangan terdiri atas barisan aritmatika dan barisan geometri . Sebelum mempelajari secara rinci atau secara mendalam , maka kita terlebih dahulu mempeljari pengertian daripada barisan bilangan .

Barisan Bilangan Aritmatika Dan Geometri 

A. Pengertian Barisan Bilangan 

Barisan bilangan yaitu suatu daftar bilangan dari sebelah kiri ke kanan yang mempunyai contoh tertentu . Setiap aggota dari barisan bilangan di sebut dengan suku bilangan atau yang biasa dilambangkan dengan ” U “

Contoh :

3,4,5,6,7,8,9,10, . . . .

1,2,4,8,16,32 ,. . . .

B. Macam – macam Barisan Bilangan 

Barisan bilangan terbagi atas dua macam yaitu :

1. Barisan bilangan Aritmatika


2. Barisan bilangan Geometri

C. Definisi Barisan Bilangan Aritmatika Dan geometri 

1. Barisan Bilangan Aritmatika ( penjumlahan ) 

Barisan bilangan aritmatika , yaitu barisan yang selisih antar suku yang berdekatan konstan atau barisan aritmatika disebut juga bilangan yang suku selanjutnya merupakan penjumlahan dari suku sebelumnya dengan rasio .

• Bentuk barisan aritmatika 

a. Barisan aritmatika berderajat satu 

Secara umum, barisan aritmatika ditulis sebagai berikut :

a , a+b , a+2b , a+3b , a+4b , . . . .

U1 = a

U2 = a+2b

U3 = a+3b

U4 = a+ 4b

U10= a + 9b

Jadi , diperoleh Rumus barisan aritmatika sebagai berikut :

• Rumus Barisan Aritmatika 

Un = a + ( n – 1 ) b 

b = Un -U(n-1)    atau     b= U(n+1) – Un 

Keterangan :

Un = suku ke n

n = banyaknya suku

a = suku pertama

b = rasio atau beda

Contoh Soal 

1. 7 , 13 , 19 , 25 , 31 , 37 , . . .

Dari barisan bilangan di atas , tentuka :

a.) a

b.) b

Penyelesaian :

a.) a = suku pertama maka a = 7

b.) b = U2 – U1

         = 13 – 7

   b   = 6

2. Suatu arisan aritmatika suku ke-3 = 13 dan suku ke -6 = 28 . Tentukan :

a.) b

b.) a

c.) U8

d.) Tulislah enam suku pertama

Penyelesaian :

Diketahui : U3 = 13 dan U6= 28

Jawab :

a. ) U3 = 13 ->> a + 2b = 13

     U6 = 28 ->> a + 5b = 28   _

                                 -3b = – 15

                                     b = -15 / -3

                                     b = 5

b.) a + 2b = 13

     a + ( 2.5) = 13

     a + 10 = 13

      a    = 3

c.) Un = a + (n-1)b

     U8 = a + 7b

            = 3 + 7 . 5

            = 38

d.) 3 ,8 , 13 , 18 , 23 , 28 , . . .

b. Barisan aritmatika berderajat dua 

Barisan aritmatika berderajat dua , yaitu barisan aritmatika yang beda atau rasionya tidak tetap dan dan apabila beda tersebut dijadikan barisan maka akan terbentuk rasio yang tetap atau mengalami dua tahap gres diketahui beda atau rasio yang sama atau tetap .

Rumus umum barisan aritmatika berderajat dua :

Un = an²  + bn + c

Contoh :

1 , 3 , 6 , 10 , 15 , .. . .

Dari barisan aritmatika diatas , tentukan :

a.) Un

b.) U20

Penyelesaian :

Barisan di atas merupakan barisan aritmatika berderajat dua , alasannya yaitu dua tahap gres sama rasionya .

Misal Un =  an²  + bn + c

U1 = 1 –> a + b + c = 1   . . . . .(1)

U2 = 3 –> 4a + 2b + c = 3 . . . (2)

U3 = 6 –> 9a + 3b + c = 6 . . .(3)

• Dari persamaan ( 2 ) dan (1 )

4a + 2b + c = 3

a + b + c = 1   _

3a + b = 2  . . . .( 4 )

• Dari persamaan ( 3 ) dan ( 2 )

9a + 3b + c = 6

4a + 2b + c = 3  _

5a + b = 3  . .  . . ( 5 )

• Dari persamaan ( 5 ) dan ( 4 )  untuk mencari nilai a

5a + b = 3

3a + b = 2  _

2a = 1

a = 1/2

• mencari nilai b  , maka gunakanlah salah satu persamaan dan kali ini semoga mempermudah maka gunakan persamaan (4 )

3a + b = 2

3.1/2 + b =2

1 1/2 + b = 2

b = 1/2

• mencari nilai c , maka gunakanlah persamaan ( 1 )

a + b + c = 1

1/2 + 1/2 + c = 1

1 + c = 1

c = 0

• mencari Un , maka gunakanlah persamaan misal , yaitu

Un =  an²  + bn + c

       = 1/2n²  + 1/2n + 0

      = 1/2 n ( n + 1 )

jadi , tanggapan nya yaitu :

a.) Un =  1/2 n ( n + 1 )

b.) U20 = . . .?

Un =  1/2 n ( n + 1 )

U20 = 1/2 .20 ( 20 + 1 )

        =  10 ( 21 ) = 210

2. Barisan Bilangan Geometri  ( perkalian ) 

Barisan Bilangan Geometri , yaitu suatu barisan bilangan yang suku – sukunya terdiri dari atau terbentuk dari perkalian antara rasio dengan suku sebelumnya .

Bentuk umum dari suatu barisan geometri yaitu :

a , a.r , a.r² , a.r³ , a.r⁴ , a.r⁵  , . . . . .

U1 = a

U2 = a.r

U3 = a.r²

U4 =  a.r³

U10 = a.r⁹

Jadi , Rumus Barisan bilangan Geometri  secara umum adalah

Un = a.r^n-1

Contoh soal :

1. Sebuah barisan geometri , diketahui U3 = 18 dan U6 = 486 . Tentukan :

a.) a dan r

b.) U7

c.) Tulislah tujuh suku pertama

Penyelesaian :

Diketahui : U3 = 18     U6 = 486

Jawab :

a.)  U3 = 18 –> a.r²  = 18

     U6 = 486  –> a.r ⁵  = 486

U6 / U3 = 486 / 18   —->  a.r ⁵  / a.r²   =  486 / 18

                                    —–> r³     =  27

                                               r = 3

 a.r²  = 18

a. 3² = 18

a = 2

b.) U7 = a.r ⁶

             = 2 .3 ⁶   = 2 . 729 = 1458

c.) tujuh suku pertama yaitu :

2 , 6 , 18 , 54 , 162 , 486 , 1458 , . . .

Rumus Suku Tengah Barisan Aritmatika

Sebagai aksesori gosip saja bahwa didalam Barisan Aritmatika yang mempunyai jumlah yang ganjil, maka diantara Barisan Aritmatika itu terdapat suatu Suku Tengah Barisan Aritmatika. Kemudian didalam Cara Mencari Suku Tengah Barisan Aritmatika tersebut sanggup kalian lihat rumusnya menyerupai dibawah ini :

U† = 1/2 (U1+Un)

Demikian , klarifikasi mengenai barisan bilangan aritmatika dan geometri . Inti atau kunci dari pembahasan kali ini yaitu bahwasannya pertama kali kita kenali bagaimana bntuk barisan aritmatika dan bagaimana bentuk barisan geometri . Setelah faham , maka selanjutnya gres pelajari bagaimana rumus – rumusnya dan apa saja komponen – komponen yang ada di dalamnya.

Sesungguhnya , untuk membedakan barisan aritmatika dan geometri sangatlah gampang yaitu apabila antara suku yang satu dengan yang lain merupakan hasil dari pembeda di tambah dengan suku sebelumnya maka bentuk ini disebut dengan barisan bilangan aritmatika. Sebaliknya , apabila suku pada suatu barisan bilangan merupakan hasil kali dari suku sebelumnya dengan pembeda maka bentuk ini disebut dengan barisan bilangan geometri.

Sumber https://rumusrumus.com

√ Deret Bilangan Aritmatika Dan Geometri Dalam Matematika

Deret Bilangan | Deret bilangan yaitu salah satu cabang ilmu dalam matematika yang masih ada hubungannya dengan barisan bilangan , yang sebelunya telah di bahas . Deret bilangan juga terdiri dari dua macam , menyerupai halnya barisan bilangan yaitu deret bilangan aritmatika dan deret bilangan geometri . Langkah awal untuk mempelajari deret bilangan aritmatika dan geometri yaitu kita harus memahami terlebih dahulu mengenai pengertian deret bilangan itu sendiri .Mari kita pelajari bersama

Deret Bilangan Aritmatika Dan geometri

A. Pengertian Dan Macam Deret Bilangan 

Deret bilangan yaitu jumlah dari suku – suku dari suatu barisan .

Jika U1 , U2 , U3 , U4 , . . . .Disebut dengan barisan bilangan , maka bentuk deret bilangan yaitu U1 + U2 + U3 +…

Contoh :

3 + 7 + 11 + 15 + . . .

Macam – macam deret bilangan yaitu :

• Deret bilangan aritmatika


• Deret bilangan geometri

B. Definisi Deret bilangan aritmatika dan deret bilangan geometri 

1. Deret Bilangan Aritmatika 

Deret aritmatika , yaitu suatu jumlah dari suku – suku barisan bilangan aritmatika .

Jika a , a+b , a+2b , a+3b , a+4b , . . . .a+(n-1)b yaitu barisan bilangan aritmatika maka bentuk dari deret aritmatika yaitu a+ (a+b) + ( a+2b) + (a+3b) + (a+4b) + . . . .

Rumus Jumlah deret aritmatika suku ke n  adalah :

Sn = 1/2  n ( a+ Un )  atau Sn = 1/2n [ 2a + ( n – 1 ) b ] 

Keterangan :

Sn = jumlah suku ke n

n = Banyaknya suku

b = rasio atau beda

Contoh soal :

1. 4 + 9 + 14 + 19 + . . .

Dari deret bilangan diatas , tentukan S30 = . . ?

Penyelesaian :

Diketahui : a = 4 , b = 5

Un = a + ( n – 1 ) b

U30 = 4 + ( 30 -1 ) 5

= 4 + 29.5

= 4 + 145

= 149

maka , S30 yaitu :

Cara 1 

Sn = 1/2  n ( a+ Un )

S30 = 1/2 . 30 ( 4 + 149 )

= 15 x 153

= 2295

Cara 2

Sn = 1/2n [ 2a + ( n – 1 ) b ]

S30 = 1/2 30 [ 2.4 + ( 30 – 1 ) 5 ]

= 15 [ 8 + 29 .5 ]

= 15 ( 8 + 145 )

= 15 ( 153 )

= 2295

2. Tentukan nilai n dan sn dari deret aritmatika dibawah ini :

3 + 7 + 11 + 15 + . . .+ 199

Penyelesaian :

Diketahui : a = 3 , b = 4

Ditanya :

a.) n = . . .

b.) Sn = . . .

Jawab :

a.) Un = a + ( n -1 ) b

199 = 3 + ( n – 1 ) 4

199 = 3 + 4n -4

199 = -1 + 4n

200 = 4n

50 = n

b.) cara 1

Sn = 1/2  n ( a+ Un )

S50 = 1/2 .50 ( 3 + 199 )

= 25 ( 202 )

= 5050

Cara 2

Sn = 1/2n [ 2a + ( n – 1 ) b ]

S50 = 1/2.50 [ 2.3 + ( 50 – 1 ) 4 ]

= 25 [ 6 + 49.4 ]

= 25 ( 6 + 196 )

= 25 ( 202 )

= 5050

3. Tentukan Sn , dari deret aritmatika berikut :

1 + 5 + 9 + 13 + . . . + U10

Penyelesaian :

Diketahui :

a = 1 , b = 4 , n = 10

Ditanya : Sn = . . . ?

Jawab :

Sn = 1/2n [ 2a + ( n – 1 ) b ]

S10 = 1/2.10 [ 2.1 + ( 10 – 1 ) 4 ]

= 5 [ 2 + 9.4 ]

= 5 ( 2 + 36 )

= 190

4. Diketahui suatu deret aritmatika suku ke5 = 13 dan suku ke 9 = 21 . Tentukan :

a.) nilai a dan b

b.) U10

c.) S11

Penyelesaian ;

a.) U5 = 13 —> a + 4b = 13

U9 = 21 —> a+ 8b = 21   _

-4 b = -8

b = 2

a + 4b = 13

a + 4.2 = 13

a + 8 = 13

a = 5

b.) U10 = a + 9b

U10 = 5 + 9 .2

u10 = 5 + 18   =  23

c.) Sn = 1/2n [ 2a + ( n – 1 ) b ]

S11  = 1/2 .11 [ 2.5 + ( 11 – 1 ) 2 ]

 S11 = 1/2 .11 [ 10 + 10.2 ]

S11 = 1/2.11 ( 30 )

S11 = 165

2. Deret Bilangan Geometri 

Deret bilangan geometri , yaitu jumlah dari barisan bilangan geometri .

Jika bentuk barisan bilangan geometri yaitu  a , a.r , a.r² , a.r³ , a.r⁴ , a.r⁵  . . . . a.r^n-1 maka bentuk dari deret bilangan geometri yaitu  a + a.r + a.r² + a.r³ + a.r⁴ + a.r⁵  . . . .a.r^n-1

Jumlah n suku pertama dari deret geometri atau yang dilambangkan dengan Sn , yaitu :

Sn = a + a.r + a.r² + a.r³ + a.r⁴ + a.r⁵  . . . .a.r^n-1

Apabila rumus di atas kita kalikan dengan r . maka akan menghasilkan rums sebagai berikut :

rSn =   a.r + a.r² + a.r³ + a.r⁴ + a.r⁵  + a.r⁶. . . .a.r^n-1  + a.rⁿ

Dari kedua persamaan diatas , kita kurangkan maka akan dihasilkan sebagai beriikut :

Sn = a + a.r + a.r² + a.r³ + a.r⁴ + a.r⁵  . . . .a.r^n-1

rSn =   a.r + a.r² + a.r³ + a.r⁴ + a.r⁵  + a.r⁶. . . .a.r^n-1  + a.rⁿ

                                                                                                                                    _

Sn – rSn = a –  a.rⁿ

Sn ( 1 – r ) = a ( 1 – rⁿ )

Sn =  a – a rⁿ  / 1 – r

Sn = a ( 1 – rⁿ ) / ( 1 – r )

Jadi , sanggup kita simpulkan bahwa , rumus jumlah n suku pertama dalam deret geometri yaitu :

Sn = a – a rⁿ  / 1 – r atau Sn = a ( 1 – rⁿ) / 1 – r  , dengan r  ≠ 1

Untuk lebih jelasnya lagi , maka perhatikan teladan – teladan soal di bawah ini :

1. Diketahui sebuah deret geoetri , dimana U3 = 18 , dan U6 = 486 . Tentukan :

a.) a dan r

b.) S10

Penyelesaian :

a.) U6 = 486 –> a.r ⁵= 486

 U3      =     18  –>  a.r²  = 18

U6 / U3 = 486 / 18   —–>  a.r ⁵ /   a.r²  =  486 / 18

                                                     r³ = 27

                                                      r = 3

a.r²  = 18   

a.3²  = 18

a.9 = 18

a = 2

b.) Sn = a ( 1 – rⁿ ) / 1 – r

S10 = 2 ( 1 – 3¹⁰ ) / ( 1 – 3 )

S10 = 2 ( -59048  ) / ( -2 )

S10 = 59048

2. Perhatikan deret bilangan geometri berikut:

2 + 6 + 18 + 54 + . . . . .+ 1458 , tentukan Sn !

Penyelesaian :

Diketahui : a = 2 dan r = 3

Jawab :

Langkah pertama mencari n terlebih dahulu , yaitu dengan cara :

Un = a.r^n-1

1458  = 2 . 3^n-1

1458 /2 = 3^n-1

729 = 3^n-1

3⁶ = 3^n-1

n – 1 = 6

n = 7

Selanjutnya , tinggal masukkan ke dalam rumus :

Sn = a ( 1 – rⁿ ) / 1 – r

S7 = 2 ( 1- 3⁷ ) / 1- 3

S7 = 2 ( 1-2187 ) / -2

S7 = 2187

Demikia klarifikasi mengenai Deret Aritmtika dan deret geometri . Inti dari deret yaitu menjumlahkan semua barisan bilangan baik aritmatika atau geometri . Semoga dengan klarifikasi di atas , sanggup membantu menuntaskan permasalahan dalam menuntaskan soal yang bekerjasama dengan deret bilangan .

Sumber https://rumusrumus.com