Halaman ini kita akan mempelajari perihal pengertian, rumus dan pola soal standar deviasi yang kita bahas memakai bahasa yang ringan dan gampang dimengerti.
Berbicara perihal standar deviasi tidak sanggup kita lepaskan dari kegiatan pengukuran. Pengukuran disini maksudnya yaitu pengukuran berulang dimana hasil ukurnya (atau yang biasa disebut sebagai data) ada banyak dan bervariasi.
Pengukurannya apa saja yang penting pengukuran berulang, contohnya mengukur tinggi tubuh siswa satu kelas, menghitung pendapatan orang satu kampung atau menghitung jumlah buah masing-masing dari 100 pohon mangga dsb.
Atau pola lainnya yang lebih berbau-bau sains contohnya mengukur besar gravitasi di kamarmu sebanyak 50 kali pengambilan data, mengukur kelembaban udara di beberapa titik di kampungmu atau mengukur besar intensitas cahaya di beberapa titik area sawah.
Nah, dari pengukuran berulang ini nantinya kita akan mendapat hasil yang berupa nilai rata-rata terbaik dari setiap pengulangan pengukuran dan nilai ralat. Nah, nilai ralat inilah yang merupakan nilai sebaran disekitar rata-rata atau yang disebut sebagai standar deviasi.

jadi apa pengertian standar deviasi itu? (Baca juga: Munguraikan komponen vektor )

Pengertian, Rumus dan Contoh Soal Standar Deviasi
A. Pengertian Standar Deviasi
Standar deviasi yaitu nilai yang menggambarkan seberapa besar perbedaan antar data (hasil pengukuran) atau persebaran datanya terhadap nilai rata-rata. Semakin besar persebaran datanya, maka nilai standar deviasinya juga semakin besar.
Begitu juga sebaliknya, semakin kecil persebaran datanya, maka standar deviasinya juga semakin kecil. Bagaimana bila data-datanya nilainya sama?, kalau datanya semua sama atau homogen, maka nilai standar deviasinya nol.
B. Rumus Standar Deviasi
Perlu kita ketahui bahwa untuk mendapat data populasi di lapangan itu sangatlah sulit. Misalnya kita ingin mendata tinggi penduduk Indonesia sesuai kategori umur dari Sabang hingga Merauke.
Baca juga: Ketidakpastian pengukuran
Nah, persoalannya –apa iya kita mau menghitung tinggi semua penduduk? hingga harus ke pelosok hutan segala?-, tentu ini sangatlah sulit. Untuk itu, cara yang paling gampang yaitu dengan mengambil data sampel yang sekiranya sanggup mewakili data populasi.
Sehingga varian atau ragam merupakan varian atau ragam sampel (bukan varian atau ragam populasi/induk). Persamaan ragam sampelnya yaitu sebagai berikut.
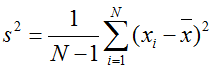
Rumus standar deviasinya yaitu sebagai berikut.

C. Contoh Soal Standar Deviasi
Telah dilakukan pengukuran intensitas cahaya sebanyak 10 kali di halaman sekolah. Diperoleh data berturut-turut sebagai berikut: 10,2; 10,5;11,0;10,6;12,0;13,0;11,5;12,5;11,3 dan 10,8 W/m2.
Baca juga: Cara mencari angka penting
Jawab
Pertama-tama kita tulis datanya di dalam tabel (supaya gampang kita sanggup melaksanakan perhitungan memakai Microsoft Excel).
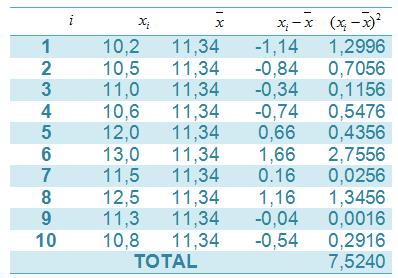
Setelah itu gunakan persamaan atau rumus ragam sampel
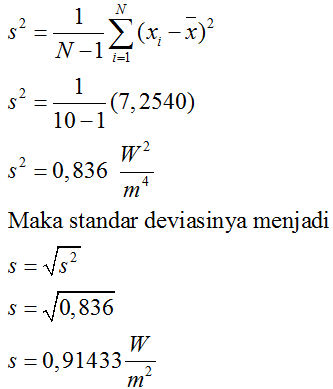
D. Fungsi atau Manfaat Standar Deviasi
Standar deviasi mempunyai beberapa manfaat diantaranya:
- Memberikan citra kepada kita perihal persebaran data terhadap data rata-rata.
- Memberikan citra kualitas data sampel yang diperoleh (apakah sanggup mewakili data populasi atau tidak?)
- Pada perhitungan fisika sanggup menunjukkan citra nilai ketidakpastian pada ketika melaksanakan pengukuran berulang.
- Dapat menunjukkan citra kepada kita perihal rentang nilai minimal dan maksimal pada data yang diperoleh.
Nah, apabila temen-temen punya pertanyaan terkait pengertian, rumus dan pola soal standar deviasi di atas sanggup ditulis di bawah ini.
Sumber https://www.siswapedia.com