Cara Menulis Besaran Vektor
Artikel ini merupakan halaman kedua pembahasan kita terkait besaran vektor. Di halaman sebelumnya kita telah mengenal besaran vektor secara ringkas. Untuk membacanya dapat klik artikel berjudul mengenal besaran vektor ini.
Seperti yang telah kita bahas sebelumnya bahwa besaran vektor mempunyai nilai dan arah yang tentu menjadikan penjumlahan pada besaran vektor menjadi berbeda dengan proses penjumlahan pada besaran skalar.
Pada besaran vektor, besar vektornya yang dilambangkan (|…| )atau abjad besar yang dibentuk miring dimana nilainya ditulis ibarat nilai skalar sedangkan arahnya ditulis memakai besarnya sudut terhadap contoh tertentu, contohnya koordinat kartesius (x,y,z). Dimana arahnya berturut-turut ditulis sebagai berikut
![]()
Menulis besaran vektor memakai koordinat kartesius
Perhatikanlah contoh di bawah ini.
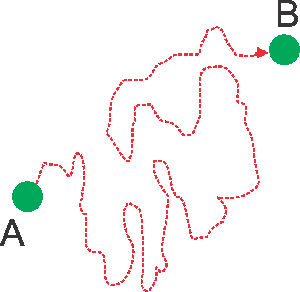
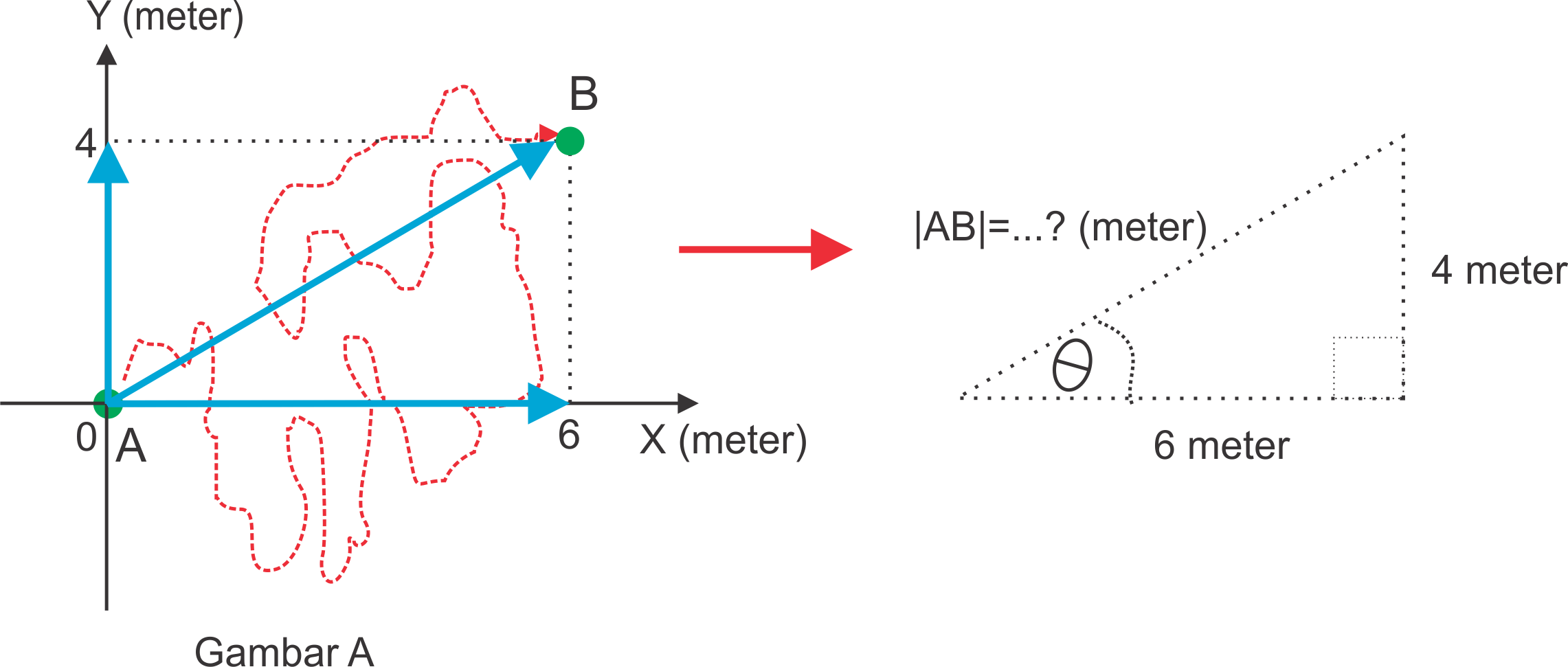
Seekor lalat terbang dari titik A dengan bentuk lintasan garis putus-putus bewarna merah ibarat pada gambar di bawah ini kemudian berhenti di titik B. Untuk mudahnya, anggap saja ini masih dalam bentuk dua dimensi sehingga kita hanya memakai contoh sumbu x dan sumbu y. Nah, bagaimana cara menulis dalam bentuk besaran vektornya?
Pertama-tama kita buat terlebih dahulu koordinatnya sehabis itu kita tentukan besarnya perpindahan dari titik A ke B di sumbu-X dan sumbu-Y. Pada contoh di atas contohnya perpindahannya di sumbu-X sebesar 6 meter dan sumbu-Y sebesar 4 meter.
Pembuatan koordinatnya bebas, tidak ada hukum baku namun yang terpenting konsisten alias dilarang berubah-ubah. Berikut kami tampilkan dua variasinya.
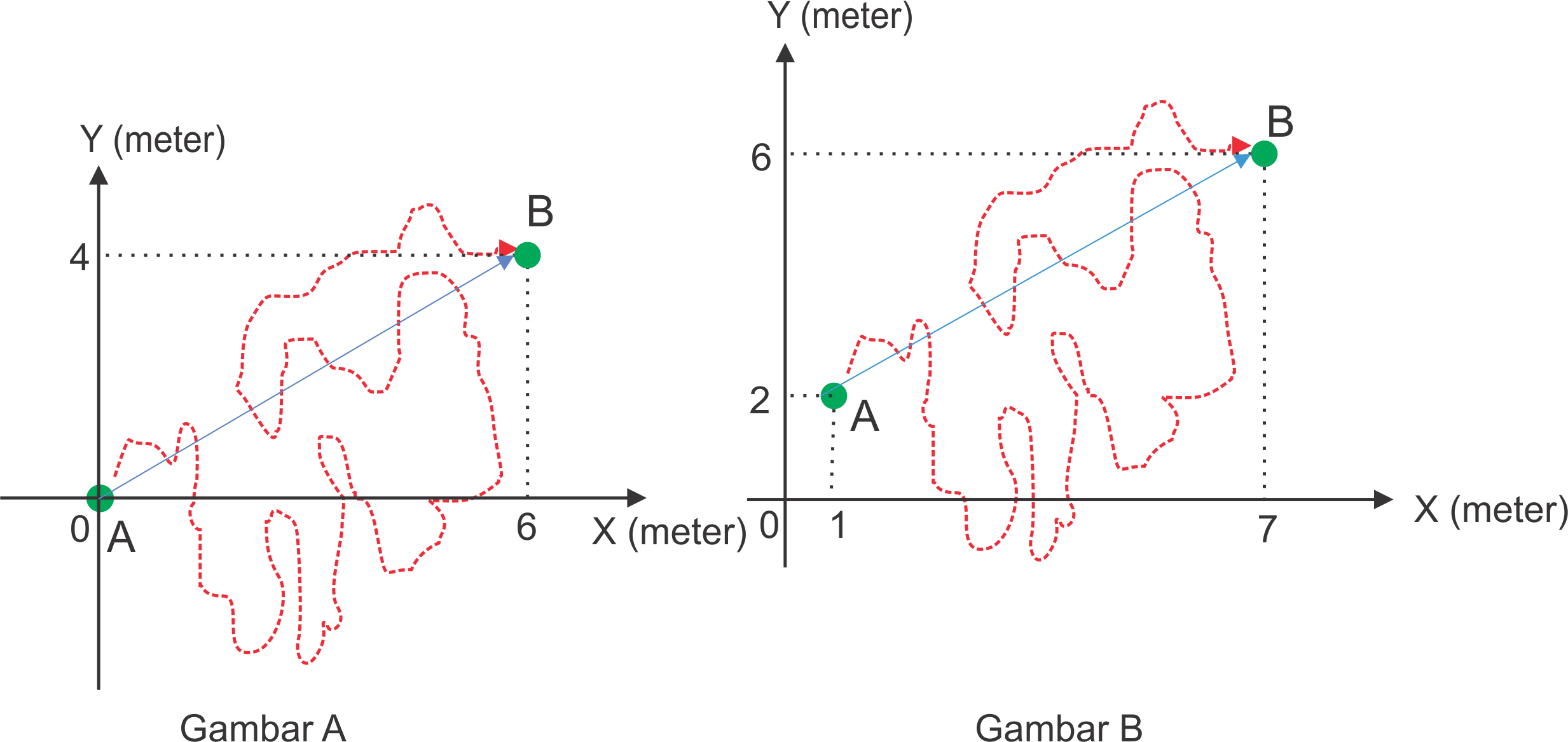
Jika memakai gambar A, maka posisi lalat di titik A dan B dapat ditullis sebagai berikut.
A = (0,0) dan B = (6,4)
Vektornya
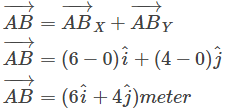
Jika memakai gambar B, maka posisi lalat di titik A dan B dapat ditullis sebagai berikut.
A = (1,2) dan B = (7,6)
Vektornya
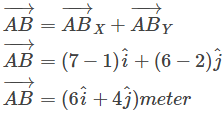
Nah, vektornya pada balasannya sama kan? Dimanapun posisi kita menaruh koordinatnya niscaya nanti besarnya akan sama.
Berapa besarnya vektor pada contoh di atas?
Teman-teman masih ingat dengan teorema Phytagoras?. Jika masih ingat, maka beruntunglah kita alasannya dengan memakai teorema ini kita akan dapat mengetahui nilai |AB|. Perhatikanlah gambar berikut ini.
Misalnya kita akan memakai gambar A, maka…
Menggunakan teorema Phytagoras, maka diperoleh besar vektornya
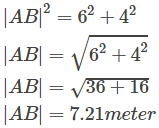
Setelah itu kita tentukan arahnya (ɵ) yaitu
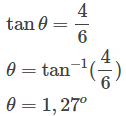
Maka kesimpulannya lalat tersebut melaksanakan perpindahan dari titik A ke titik B sejauh 7.21 meter dengan arah 1,27o dari permukaan sumbu-X. Dalam kehidupan sehari-hari, sumbu-X dapat berupa lantai yang datar, atas meja, permukaan maritim atau yang lainnya.
Sumber https://www.siswapedia.com